Giải bài 3.5 trang 42 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

Cho tam giác ABC có a = 6, b = 5, c = 8. Tính cosA, S, r.

Phân tích và Hướng dẫn giải

Bài toán yêu cầu chúng ta tính ba đại lượng: $\cos A$, diện tích $S$ và bán kính đường tròn nội tiếp $r$ của tam giác ABC khi biết độ dài ba cạnh $a,b,c$.

• Tính $\cos A$: Chúng ta sẽ sử dụng định lý cosin để tính $\cos A$. Công thức định lý cosin cho góc A là: a²=b²+c²−2bccosA. Từ đó, ta có thể suy ra công thức tính $\cos A$.

• Tính diện tích $S$: Chúng ta có thể dùng công thức Heron để tính diện tích tam giác khi biết độ dài ba cạnh. Công thức này yêu cầu tính nửa chu vi $p$ của tam giác trước.

• Tính bán kính $r$: Sau khi đã có diện tích $S$ và nửa chu vi $p$, ta có thể sử dụng công thức liên hệ giữa diện tích và bán kính đường tròn nội tiếp: $S=p\cdot r$. Từ đó, ta suy ra công thức tính $r$

Lời giải chi tiết:

Ta có hình minh họa như sau:

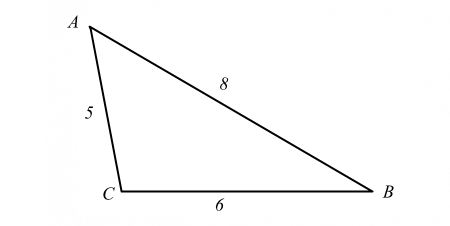
• Xét ΔABC:

- Theo định lý hàm cos ta có:

- Diện tích ΔABC là:

(đvdt)

- Nửa chu vi của ΔABC là:

- Mà S = pr nên ta suy ra:

Vậy cosA = 0,6625, S = 14,98 đvdt, r = 1,58.