Giải bài 3.8 trang 42 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

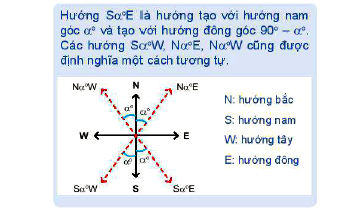
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S70°E với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.

a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.

b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

Phân tích và Hướng dẫn giải:

Để giải quyết bài toán này, chúng ta sẽ mô hình hóa chuyển động của tàu bằng một tam giác trong mặt phẳng tọa độ.

• Quãng đường thứ nhất: Tàu đi từ A đến B theo hướng S70°E.

• Quãng đường thứ hai: Tàu trôi từ B đến C theo hướng nam.

• Khoảng cách cần tìm: Khoảng cách từ A đến C chính là độ dài cạnh AC của tam giác ABC.

Các bước giải quyết:

1. Tính độ dài các cạnh: Sử dụng công thức $s=v\cdot t$ để tính độ dài hai quãng đường AB và BC.

2. Tính góc B: Xác định góc  của tam giác. Dựa vào hướng di chuyển của tàu, ta có thể tính được góc này từ các góc đồng vị, so le trong, hoặc kề bù.

3. Tính khoảng cách AC: Sử dụng định lý cosin cho tam giác ABC để tính độ dài cạnh AC.

4. Xác định hướng: Sử dụng định lý sin để tìm góc . Dựa vào góc này và hướng ban đầu (S70°E), ta sẽ xác định được hướng từ A đến C.

Lời giải chi tiết:

Ta có sơ đồ di chuyển của tàu như sau:

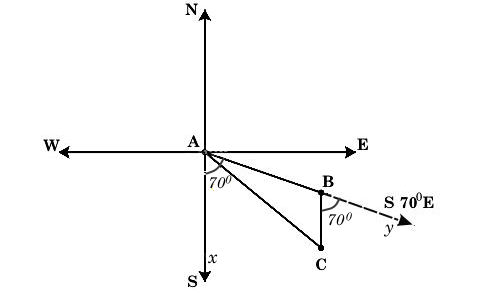
Tàu cá xuất phát từ A đi theo hướng S70⁰E với vận tốc 70km/h trong 90 phút = 1,5 giờ thì tàu cá đi được đến B (vị trí tàu bị hỏng), quãng đường AB là: 70.1,5 = 105 (km).

Từ vị trí B tàu cá trôi tự do với vận tốc 8km/h theo hướng nam sau 2h thì neo đậu vào đảo C, khi đó quãng đường BC là: 8.2 = 16km.

Khoảng cách từ cảng A đến nơi tàu neo đậu chính là đoạn AC.

Do tàu đi theo hướng S70⁰E nên phương AB hợp với phương nam Ax một góc 70⁰ nên:  

Mà phương BC song song với phương nam Ax nên:

(hai góc đồng vị)

 (góc  kề bù với góc )

Xét ΔABC, theo định lý cosin ta có:

AC² = AB² + AC² – 2AB.AC.cosB

= 105² + 16² – 2.105.16.cos110⁰

≈ 12 430,19

⇒ AC ≈ 111,49 km.

Vậy khoảng cách từ cảng A đến đảo nơi tàu neo đậu khoảng 111,49 km.

b) Xét ΔABC, ta có:

Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62,25⁰E.