Giải bài 3.11 trang 43 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

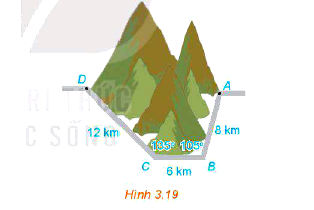
Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ.

Phân tích và Hướng dẫn giải:

Để giải quyết bài toán này, chúng ta cần tìm độ dài của đường mới (đoạn AD) và so sánh với độ dài đường cũ (đoạn AB + BC + CD). Vì đường mới đi xuyên qua núi, ta có thể mô hình hóa bài toán thành việc tính độ dài một cạnh trong một hình tứ giác.

Các bước giải quyết:

1. Tính độ dài đường cũ: Đây là tổng độ dài các đoạn đường AB, BC và CD.

2. Tính độ dài đường mới (đoạn AD):

   • Ta không thể tính trực tiếp AD từ tứ giác ABCD. Thay vào đó, ta sẽ chia tứ giác này thành hai tam giác (ABC và ACD).

   • Sử dụng định lý cosin cho tam giác ABC để tính độ dài cạnh AC.

   • Sử dụng định lý sin cho tam giác ABC để tính góc .

   • Tính góc  dựa trên góc đã biết.

   • Cuối cùng, sử dụng định lý cosin cho tam giác ACD để tính độ dài cạnh AD.

3. So sánh: Lấy độ dài đường cũ trừ đi độ dài đường mới để tìm ra độ dài đã giảm.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

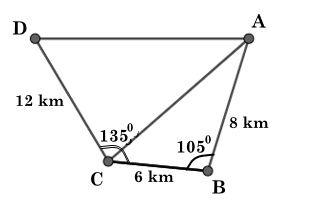
Xét ΔABC, có:

AC² = AB² + BC² – 2AB.BC.cosB (định lí cos)

= 8² + 6² – 2.8.6.cos105⁰ ≈ 124,85

⇒ AC ≈ 11,17 km.

Theo định lý hàm sin, ta có:

Xét ΔADC, theo định lý hàm cos, ta có:

AD² = AC² + DC² – 2AC.DC.

= 11,17² + 12² – 2.11,17.12.cos91,23⁰ ≈ 274,52

⇒ AD ≈ 16,57 km.

Độ dài đoạn đường cũ là:

AB + BC + CD = 8 + 6 + 12 = 26 km.

Độ dài đường cũ hơn độ dài đoạn đường mới:

26 – 16,57 = 9,43 km.

Vậy độ dài đường mới giảm 9,43 km so với đoạn đường cũ.