Giải bài 2.15 trang 32 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu: trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm.

Vì lí do giảm thuế, bác An muốn số tiền đầu tư lãi suất chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng. Hơn nữa, để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp. Hỏi bác An nên đầu tư mỗi loại trái phiếu bao nhiêu tiền để lợi nhuận thu được sau một năm là lớn nhất?

Phân tích và Hướng dẫn giải:

Đây là một bài toán tìm cách để đạt được giá trị lớn nhất (lợi nhuận) trong một số điều kiện ràng buộc (tổng vốn, tỷ lệ đầu tư, giới hạn rủi ro). Để giải quyết bài toán này, ta sẽ làm theo các bước sau:

1. Lập mô hình toán học: Biến đổi các điều kiện của bài toán thành một hệ bất phương trình bậc nhất hai ẩn.

2. Xác định hàm lợi nhuận: Viết biểu thức tính tổng lợi nhuận thu được.

3. Biểu diễn miền nghiệm: Vẽ các đường thẳng tương ứng với các bất phương trình để tìm ra miền nghiệm. Miền nghiệm này chính là tập hợp tất cả các phương án đầu tư hợp lệ.

4. Tìm phương án tối ưu: Tính giá trị của biểu thức lợi nhuận tại các đỉnh của miền nghiệm. Giá trị lớn nhất sẽ đạt được tại một trong các đỉnh đó.

Lời giải chi tiết:

Gọi số tiền bác An đầu tư cho trái phiếu chính phủ, trái phiếu ngân hàng lần lượt là: x, y (triệu đồng) (0 ≤ x, y ≤ 1 200).

Khi đó bác An đầu tư cho trái phiếu doanh nghiệp là:

1 200 – x – y (triệu đồng)

Vì lí do giảm thuế, bác An muốn số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên ta có:

x ≥ 3y hay x – 3y ≥ 0.

Để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên ta có:

1 200 – x – y ≤ 200 hay x + y ≥ 1 000.

Từ đó ta có hệ bất phương trình:

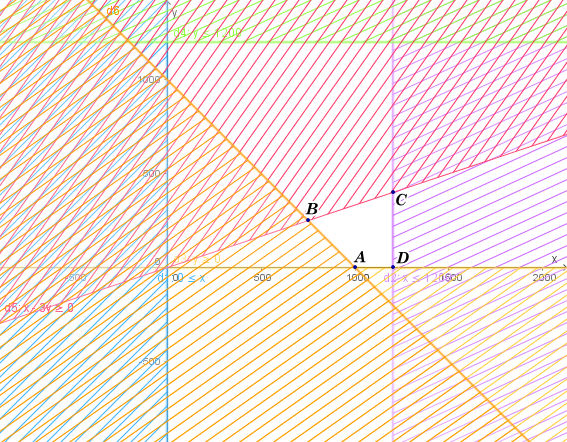
Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD với tọa độ các điểm

A(1 000; 0), B(750; 250), C(1 200; 400), D(1 200; 0).

Lợi nhuận bác An thu được là:

F(x; y) = 7%x + 8%y + 12%(1200 – x – y)

=  144 – 0,05x – 0,04y (triệu đồng)

Tính giá trị của F(x; y) tại các điểm A, B, C, D, ta được:

F(1 000; 0) = 144 – 0,05.1 000 – 0,04.0 = 94;

F(750; 250) = 144 – 0,05.750 – 0,04.250 = 96,5;

F(1 200; 400) = 144 – 0,05.1 200 – 0,04.400 = 68;

F(1 200; 0) = 144 – 0,05.1 200 – 0,04.0 = 84;

⇒ Hàm F(x; y) lớn nhất bằng 96,5 khi x = 750, y = 250.

Vậy bác An nên đầu tư 750 triệu vào trái phiếu chính phủ, 250 triệu vào trái phiếu ngân hàng và 1 200 - 750 - 250 = 200 triệu vào trái phiếu doanh nghiệp để lợi nhuận thu được là lớn nhất.