Giải bài 3.15 trang 44 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

Cho tam giác ABC có , AC = 10. Tính a, R, S, r.

Phân tích và Hướng dẫn giải:

Để giải quyết bài toán này, chúng ta sẽ thực hiện theo các bước sau:

1. Tìm góc A: Tổng ba góc trong một tam giác bằng 180∘.

2. Tính R và a: Sử dụng định lý sin:. Ta có $b=AC=10$.

3. Tính c: Tiếp tục sử dụng định lý sin để tìm cạnh c: .

4. Tính S: Sử dụng công thức diện tích tam giác:  hoặc các công thức khác.

5. Tính r: Sử dụng công thức tính bán kính đường tròn nội tiếp: $S=p\cdot r$, với $p$ là nửa chu vi tam giác.

Lời giải chi tiết:

Ta có hình minh họa như sau:

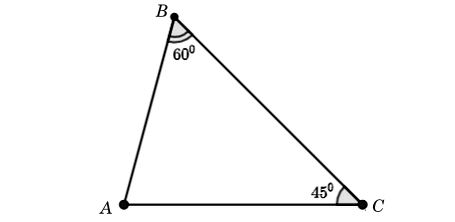
Xét ΔABC, có:

Lưu ý: a = BC; b = AC; c = AB

Theo định lý hàm sin ta có:

Diện tích ΔABC là:

Mà: 

Ta có: 

Vậy