Giải bài 3.16 trang 44 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

a) 

b) MA² + MB² – AB² = 2MA.MB. và MA² + MC² – AC² = 2MA.MC.

c) (công thức đường trung tuyến).

Phân tích và Hướng dẫn giải:

Để chứng minh các hệ thức này, chúng ta sẽ áp dụng các định lý và tính chất cơ bản của tam giác và đường trung tuyến.

• Phần a: Góc  và  là hai góc kề bù (tổng bằng 180∘). Ta sẽ sử dụng tính chất của hai góc bù nhau: cos(180^∘−α)=−cosα.

• Phần b: Đây là dạng biến đổi của định lý cosin. Ta sẽ áp dụng định lý này cho hai tam giác $\Delta AMB$ và $\Delta AMC$.

• Phần c: Đây là công thức đường trung tuyến, một công thức rất quan trọng. Ta sẽ chứng minh nó bằng cách cộng hai hệ thức đã chứng minh ở phần b) và sử dụng kết quả từ phần a).

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

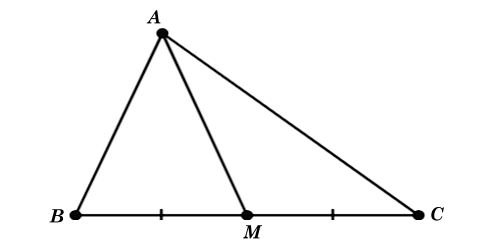a) 

Ta có: 

b) Xét ΔAMB, ta có:

AB² = MA² + MB² – 2MA.MB.

⇔ MA² + MB² – AB² = 2MA.MB.  (*)

Xét ΔAMC, ta có:

AC² = MA² + MC² – 2MA.MC.

⇔ MA² + MC² – AC² = 2MA.MC.  (**)

c) Cộng vế với vế của (*) với (**), ta được:

MA² + MB² – AB² + MA² + MC² – AC² = 2MA.MB. + 2MA.MC.

(Vì )

 (Vì )

(công thức đường trung tuyến).