Giải bài 3.18 trang 45 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

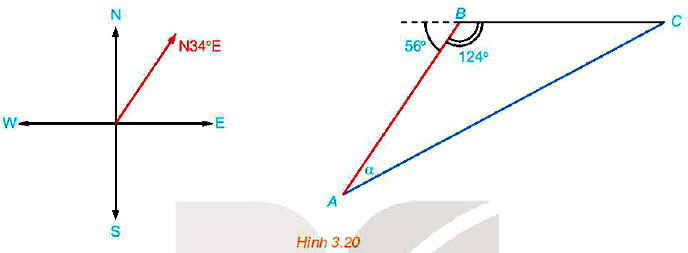
Trên biển, tàu B ở vị trí cách tàu A 53 km về hướng N34°E. Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để gặp tàu B.

a) Hỏi tàu A cần phải chuyển động theo hướng nào?

b) Với hướng chuyển động đó thì sau bao lâu tàu A gặp tàu B?

Lời giải chi tiết:

a) Gọi thời gian tàu A gặp tàu B ở vị trí C là x (h) (x > 0).

Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h đến C nên quãng đường BC là 30x (km).

Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B nên quãng đường AC là 50x (km).

Đặt 

Vì tàu B ở vị trí cách tàu A về hướng N34°E và tàu B chạy về hướng đông nên tàu A chạy từ A theo hướng N(34 + α)°E.

Theo định lí sin trong ΔABC, ta có: 

Với: α ≈ 30° (nhận)

α ≈ 150° (loại do tổng ba góc trong tam giác bằng 180°).

Vậy tàu A chuyển động theo hướng N64°E để gặp tàu B.

b) Xét ΔABC, ta có:

Theo định lí sin, ta có: 

Mà BC = 30x, AB = 53, 

Nên có: 

Vậy sau khoảng 2 giờ chạy theo hướng N64°E thì tàu A gặp tàu B.