Giải bài 3.19 trang 45 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

Trên sân bóng chày dành cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2(Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2 và cách gôn nhà 18,44m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

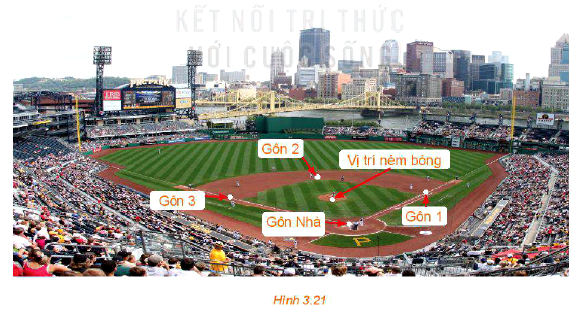
Phân tích và Hướng dẫn giải:

Để giải bài toán này, chúng ta sẽ mô hình hóa sân bóng chày bằng một hình học phẳng.

• Gọi các vị trí Gôn Nhà, Gôn 1, Gôn 2, Gôn 3 lần lượt là các đỉnh A, B, C, D của hình vuông ABCD.

• Vị trí đứng ném bóng là điểm E, nằm trên đường chéo AC và cách A một khoảng 18,44m.

• Ta cần tính khoảng cách từ E đến Gôn 1 (EB) và từ E đến Gôn 3 (ED).

Các bước giải:

1. Tính khoảng cách EB:

   • Xét tam giác ABE. Ta đã biết độ dài cạnh AB và AE.

   • Góc  là góc tạo bởi cạnh và đường chéo của hình vuông, do đó có giá trị là 45∘.

   • Áp dụng định lý cosin cho tam giác ABE để tìm độ dài cạnh EB.

2. Tính khoảng cách ED:

   • Ta có thể chứng minh $\Delta ABE=\Delta ADE$ bằng trường hợp cạnh - góc - cạnh (c.g.c).

   • Từ đó suy ra $EB=ED$.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

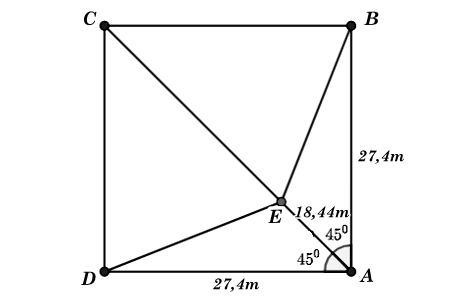
A là vị trí gôn Nhà, B là vị trí gôn 1, C là vị trí gôn 2, D là vị trí gôn 3, E là vị trí ném bóng.

Khi đó ABCD là hình vuông nên đường chéo AC là tia phân giác của góc BAD hay AE là tia phân giác của góc BAD.

• Xét ΔABE, có:

BE² = AB² + AE² – 2.AB.AE. (định lí côsin)

⇔ BE² = 27,4² + 18,44² – 2.27,4.18,44.cos45⁰

⇔ BE² ≈ 376,25

⇔ BE ≈ 19,4 m.

• Xét ΔABE và ΔADE, có:

AB = AD (gt)

AE chung

⇒ ΔABE = ΔCDE (c – g – c)

⇒ BE = DE (hai cạnh tương ứng)

⇒ DE = BE ≈ 19,4 m.

Vậy khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3 xấp xỉ bằng 19,4 m.