Hotline 0936685849

Giải bài 3.3 trang 37 Toán 10 Tập 1 SGK Kết nối tri thức

20:56:4008/08/2023

Chào các bạn! Bài 3.3 trang 37 sách giáo khoa Toán 10 (Kết nối tri thức) là một bài tập chứng minh các hệ thức lượng giác cơ bản. Đây là những công thức nền tảng và cực kỳ quan trọng, giúp các bạn giải quyết các bài toán phức tạp hơn sau này. Chúng ta sẽ chứng minh từng công thức một cách chi tiết và dễ hiểu nhất.

Đề bài:

Chứng minh các hệ thức sau:

a) sin²α + cos²α = 1;

b) $\small 1+tan^2\alpha =\frac{1}{cos^2\alpha }\: (\alpha \neq 90^0)$

c) $\dpi{100} \small 1+cot^2\alpha =\frac{1}{sin^2\alpha }\: (0^0<\alpha < 180^0)$

Phân tích và Hướng dẫn giải:

Để chứng minh các hệ thức này, chúng ta cần dựa vào định nghĩa của các tỉ số lượng giác trên đường tròn đơn vị và các công thức liên hệ cơ bản.

Phần a: Dựa vào định nghĩa $sin α$ và $cos α$ trên đường tròn đơn vị và sử dụng định lý Pythagoras trong tam giác vuông.
Phần b và c: Sử dụng công thức ở phần a để biến đổi vế trái của mỗi hệ thức. Cần nhớ định nghĩa của $tan α = s i n α/ c o s α$ và $cot α = c o s α/ s i n α$ .

Lưu ý rằng các điều kiện của góc $α$ ( $α\neq 9 0^{\circ}$ , 0 $^{\circ}$ < α < 180^∘) đảm bảo rằng các biểu thức có nghĩa.

Lời giải chi tiết:

a) Lấy điểm M trên nửa đường tròn đường tròn đơn vị sao cho $\small \widehat{xOM}=\alpha$ Từ M kẻ MH ⊥ Ox và MK ⊥ Oy như hình sau:

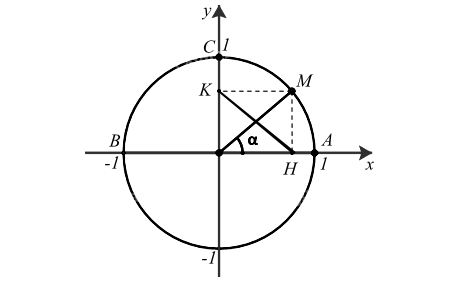
Giải bài 3.3 trang 37 Toán 10 Tập 1 SGK Kết nối tri thức

Khi đó:

OH = |cosα| , OK = |sinα| = sinα.

Xét tam giác OHK vuông tại O, ta có:

OH² + OK² = HK² (định lí Pythagore)

Mà HK = OM = 1 (tứ giác OHMK là hình chữ nhật)

Do đó, OH² + OK² = 1

⇒ |cosα|² + (sinα)² = 1

hay sin²α + cos²α = 1 (đpcm).

b) Chứng minh: $\small 1+tan^2\alpha =\frac{1}{cos^2\alpha }\: (\alpha \neq 90^0)$

Ta có: $\dpi{100} \small 1+tan^2\alpha =1+\left ( \frac{sin\alpha }{cos\alpha } \right )^2$

$\small =1+\frac{sin^2\alpha }{cos^2\alpha }=\frac{cos^2\alpha +sin^2\alpha }{cos^2\alpha }$ $\small =\frac{1}{cos^2\alpha }\: \: (\alpha \neq 90^0)$

c) Chứng minh: $\dpi{100} \small 1+cot^2\alpha =\frac{1}{sin^2\alpha }\: (0^0<\alpha < 180^0)$

Ta có: $\dpi{100} \small 1+tan^2\alpha =1+\left ( \frac{cos\alpha }{sin\alpha } \right )^2$

$\dpi{100} \small =1+\frac{cos^2\alpha }{sin^2\alpha }=\frac{sin^2\alpha +cos^2\alpha }{sin^2\alpha }$ $\dpi{100} \small =\frac{1}{sin^2\alpha }\: \: (0<\alpha < 180^0)$

Các hệ thức trên là ba trong số những công thức lượng giác cơ bản nhất.

Công thức Pythagoras lượng giác ( $\sin^2\alpha+\cos^2\alpha=1$ ) là nền tảng để suy ra các công thức còn lại.
Công thức ( $1+\tan^2\alpha=\frac{1}{\cos^2\alpha}$ ) và ( $1+\cot^2\alpha=\frac{1}{\sin^2\alpha}$ ) rất hữu ích khi biến đổi các biểu thức lượng giác, đặc biệt khi cần chuyển đổi giữa các hàm số.
Việc nắm vững và ghi nhớ các công thức này sẽ giúp bạn tự tin hơn khi giải quyết các bài toán lượng giác trong chương trình học.