Giải bài 3.6 trang 42 Toán 10 Tập 1 SGK Kết nối tri thức

Bài 3.6 trang 42 Toán 10 Tập 1 SGK Kết nối tri thức:

Cho tam giác ABC có a = 10, ,  Tính R, b, c.

Giải bài 3.6 trang 42 Toán 10 Tập 1 SGK Kết nối tri thức:

Ta có hình minh họa như sau:

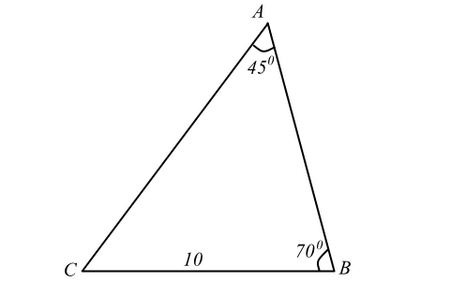
• Xét ΔABC:

- Theo định lý hàm sin ta có:

- Mặt khác, ta có: 

- Trong ΔABC, thì: 

- Theo định lý hàm số sin thì: 

Vậy , b = 13,29, c = 12,82.