Giải bài 2.16 trang 32 Toán 10 Tập 1 SGK Kết nối tri thức

Đề bài:

Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới trong một tháng trên các đài phát thanh và truyền hình. Biết cùng một thời lượng quảng cáo, số người mới quan tâm đến sản phẩm trên truyền hình gấp 8 lần trên đài phát thanh, tức là quảng cáo trên truyền hình có hiệu quả gấp 8 lần trên đài phát thanh.

Đài phát thanh chỉ nhận được quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây với chi phí là 80 nghìn đồng/giây. Đài truyền hình chỉ nhận được các quảng cáo có tổng thời lượng tối đa trong một tháng tối đa là 360 giây với chi phí là 400 nghìn đồng/giây. Công ty cần đặt thời gian quảng cáo trên các đài phát thanh và truyền hình như thế nào để hiệu quả nhất?

Gợi ý: Nếu coi hiệu quả khi quảng cáo 1 giây trên đài phát thanh là 1 (đơn vị) thì hiệu quả khi quảng cáo 1 giây trên đài truyền hình là 8 (đơn vị). Khi đó hiệu quả quảng cáo x (giây) trên đài phát thanh và y (giây) trên truyền hình là F(x, y) = x + 8y. Ta cần tìm giá trị lớn nhất của hàm F(x, y) với x, y thỏa mãn các điều kiện trong đề bài.

Phân tích và Hướng dẫn giải:

Đây là một bài toán tìm cách để đạt được giá trị cao nhất (hiệu quả quảng cáo) trong một số điều kiện ràng buộc (thời lượng và chi phí). Để giải quyết, ta sẽ đi theo các bước sau:

1. Lập mô hình toán học: Biến đổi các điều kiện của bài toán thành một hệ bất phương trình bậc nhất hai ẩn.

2. Xác định miền nghiệm: Vẽ các đường thẳng tương ứng với các bất phương trình để tìm ra miền nghiệm. Miền nghiệm này chính là tập hợp tất cả các phương án quảng cáo hợp lệ.

3. Tìm phương án tối ưu: Tính giá trị của biểu thức hiệu quả $F(x,y)$ tại các đỉnh của miền nghiệm. Giá trị lớn nhất sẽ đạt được tại một trong các đỉnh đó.

Lời giải chi tiết:

Gọi x (giây) là thời lượng quảng cáo trong một tháng công ty đặt trên đài truyền hình và y (giây) là thời lượng quảng cáo trong một tháng công ty đặt trên đài phát thanh. (0 ≤ x ≤ 360, 0 ≤ y ≤ 900).

Chi phí công ty chi trả cho quảng cáo trong một tháng là:

400x + 80y (nghìn đồng)

Vì công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới nên ta có:

400x + 80y ≤ 160 000

hay 5x + y ≤  2 000.

Khi đó ta có hệ bất phương trình:

Miền nghiệm của hệ bất phương trình là ngũ giác OABCD với tọa độ các điểm là O(0; 0), A(0; 900), B(220; 900), C(360; 200), D(360; 0).

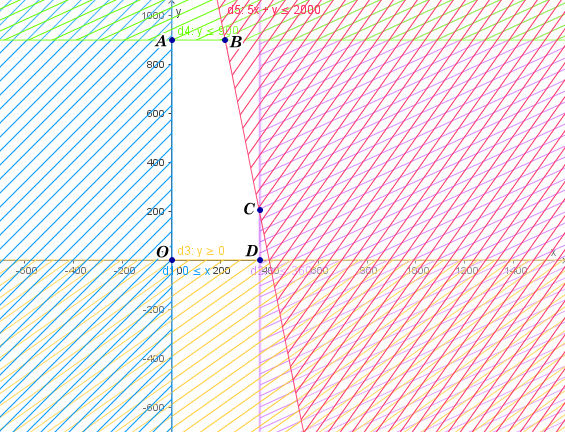
Nếu coi hiệu quả khi quảng cáo 1 giây trên đài phát thanh là 1 (đơn vị) thì hiệu quả khi quảng cáo 1 giây trên đài truyền hình là 8 (đơn vị). Khi đó hiệu quả quảng cáo x (giây) trên đài phát thanh và y (giây) trên truyền hình là F(x; y) = x + 8y.

Tính giá trị F(x,y) tại các điểm O, A, B, C, D, ta có:

F(0; 0) = 0 + 8.0 = 0;

F(0; 900) = 0 + 8.900 = 7 200;

F(220; 900) = 220 + 8.900 = 7 420;

F(360; 200) = 360 + 8.200 = 1 960;

F(360; 0) = 360 + 8.0 = 360;

⇒ Hàm F(x; y) đạt giá trị lớn nhất bằng 7 420 tại x = 220, y = 900.

Vậy công ty cần đặt thời gian quảng cáo 900 giây trên các đài phát thanh và 220 giây trên đài truyền hình để đạt hiệu quả cao nhất.