Bài 8 trang 27 Toán 8 Tập 2 Chân trời sáng tạo

Đề bài:

Lan phụ giúp mẹ bán nước chanh, em nhận thấy số li nước chanh y bán được trong ngày và nhiệt độ trung bình x (°C) của ngày hôm đó có mối tương quan. Lan ghi lại các giá trị tương ứng của hai đại lượng x và y trong bảng sau:

a) So sánh các giá trị x và y tương ứng trong bảng dữ liệu trên với tọa độ (x; y) của các điểm A, B, C, D, E, F trên mặt phẳng tọa độ trong Hình 6.

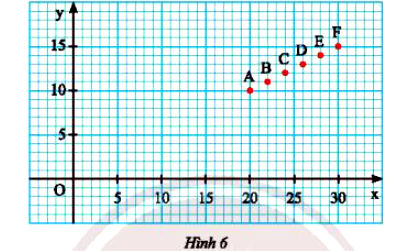
b) Cho biết đường thẳng d: y = mx đi qua các điểm A, B, C, D, E, F ở câu a. Tìm hệ số góc của d.

Phân tích và Hướng dẫn giải:

a) So sánh tọa độ: Ta so sánh các cặp $(x; y)$ trong bảng với tọa độ của các điểm $A, B, C, D, E, F$.

b) Tìm hệ số góc $m$: Đường thẳng $y = mx$ đi qua các điểm này, nghĩa là tỉ số $\frac{y}{x}$ của mọi điểm đều bằng hệ số góc $m$. Ta chọn một cặp $(x; y)$ bất kỳ (ví dụ, điểm $A(20; 10)$) và thay vào công thức để tìm $m$.

Lời giải chi tiết:

a) Các giá trị x và y tương ứng trong bảng dữ liệu là tọa độ (x; y) của các điểm A, B, C, D, E, F trên mặt phẳng tọa độ trong Hình 6 ở trên.

b) Đường thẳng d: y = mx đi qua các điểm A có tọa độ (20; 10) nên thay vào đường thẳng ta có:

10 = m.20

Suy ra: m = 1/2

Vậy hệ số góc của d là  1/2.