Bài 7.32 SGK Toán 11 Tập 2 Kết nối tri thức

Bài 7.32 SGK Toán 11 Tập 2 Kết nối tri thức:

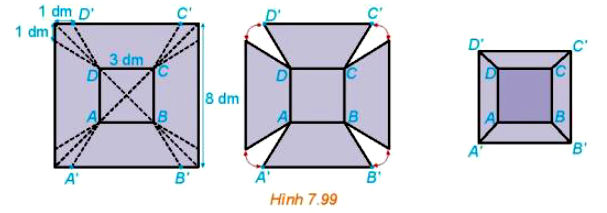
Từ một tấm tôn hình vuông có cạnh 8 dm, bác Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không có nắp) như Hình 7.99.

a) Giải thích vì sao chiếc thùng có dạng hình chóp cụt.

b) Tính cạnh bên của thùng.

c) Hỏi thùng có thể chứa được nhiều nhất bao nhiêu lít nước?

Giải bài 7.32 SGK Toán 11 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

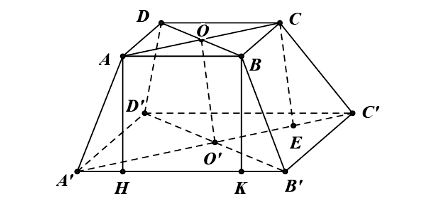
a) Có AB // A'B' nên AB // (A'B'C'D').

AD // A'D' nên AD // (A'B'C'D'). Do đó (ABCD) // (A'B'C'D').

Vì bác Hùng cắt bỏ bốn phần như nhau ở bốn góc và hàn lại sẽ tạo thành 4 mặt bên là các hình thang cân. Vậy chiếc thùng có dạng hình chóp cụt.

b) Dựa vào hình 7.99, ta có A'B' = B'C' = C'D' = D'A' = 8 – 2 = 6 (dm).

Kẻ AH ⊥ A'B' tại H, Kẻ BK ⊥ A'B' tại K.

Khi đó ABKH là hình chữ nhật, suy ra AB = HK = 3 dm,

AH = BK = (8 – 3) : 2 = 2,5 dm.

Xét ΔAHA' và ΔBKB' có

AA' = BB',

AH = BK.

Nên: ΔAHA' = ΔBKB',

⇒ A'H = B'K = (A'B' – HK)/2 = (6 – 3)/2 = 1,5 (dm).

Xét tam giác AHA' vuông tại H, có AA' = :

Vậy cạnh bên của thùng là 

c) Gọi O và O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'.

Vì ACC'A' là hình thang cân nên đường cao của hình chóp cụt cũng chính là đường cao của hình thang cân.

Kẻ CE ⊥ A'C' tại E.

Vì OCEO' là hình chữ nhật nên OC = O'E.

Xét tam giác ABC vuông tại B có

Mà O là trung điểm của AC nên:

Xét tam giác A'B'C' vuông tại B' có:

Mà O' là trung điểm của A'C' nên:

Có C'E = O'C' – O'E 

Xét tam giác CC'E vuông tại E, có:

⇒ OO' = 2 dm

Ta có S₁ = S_ABCD = 3 . 3 = 9 (dm²); S₂ = S_A'B'C'D' = 6 . 6 = 36 (dm²).

Khi đó:

Ta có 42 dm³ = 42 lít.

Vậy thùng có thể chứa được nhiều nhất là 42 lít nước.