Bài 7.25 trang 59 Toán 11 tập 2 Kết nối tri thức

Bài 7.25 trang 59 Toán 11 Tập 2 Kết nối tri thức:

Cho hình lập phương ABCD.A'B'C'D'có cạnh a.

a) Chứng minh rằng hai mặt phẳng (D'AC)và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.

b) Xác định các giao điểm E, F của DB' với (D'AC), (BC'A'). Tính d((D'AC), (BC'A')).

Giải bài 7.25 trang 59 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

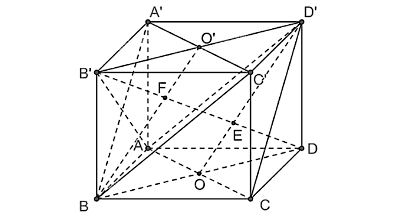
a) Vì AA' // CC' và AA' = CC' (do chúng cùng song song và bằng BB') nên AA'C'C là hình bình hành,

⇒ AC // A'C' do đó A'C' // (D'AC).

Vì AB // C'D' và AB = C'D' (do chúng cùng song song và bằng CD) nên ABC'D' là hình bình hành

⇒ BC' // AD', do đó BC' // (D'AC).

Vì A'C' // (D'AC) và BC' // (D'AC) nên (BC'A') // (D'AC).

Vì ABCD là hình vuông nên AC ⊥ BD.

Vì BB' ⊥ (ABCD) nên BB' ⊥ AC mà AC ⊥ BD nên AC ⊥ (BB'D),

⇒ AC ⊥ DB'.

Vì AC // A'C' mà AC ⊥ DB' nên A'C' ⊥ DB'.

Do AD ⊥ (ABB'A') nên AD ⊥ A'B.

Vì ABB'A' là hình vuông nên AB' ⊥ A'B mà AD ⊥ A'B nên A'B ⊥ (ADB').

⇒ A'B ⊥ DB'.

Có A'C'  ⊥ DB' và A'B ⊥ DB' nên DB' ⊥ (BC'A').

Vì A'D' // BC và A'D' = BC (do chúng cùng song song và bằng AD) nên A'D'CB là hình bình hành,

⇒ A'B // D'C

mà A'B ⊥ DB' nên D'C ⊥ DB'.

Có AC ⊥ DB' và D'C ⊥ DB' nên DB' ⊥ (D'AC).

b) Gọi O và O' lần lượt là tâm của hai hình vuông ABCD và A'B'C'D'.

Trong mặt phẳng (BDD'B'), có DB' ∩ D'O = E.

Khi đó DB' ∩ (D'AC) = E.

Trong mặt phẳng (BDD'B'), có DB' ∩ BO' = F.

Khi đó DB' ∩ (BC'A') = F.

Vì (BC'A') // (D'AC) nên d((D'AC), (BC'A')) = d(E, (BC'A')) = EF (vì DB' ⊥ (BC'A')).

Vì DB' ⊥ (BC'A') nên DB' ⊥ BO' và DB' ⊥ (D'AC) nên DB' ⊥ D'O,

⇒ BO' // D'O.

Xét tam giác DBF, có OE // BF nên theo định lí Thalés, ta có: 

Xét tam giác B'D'E có O'F // D'E nên theo định lí Thalés, ta có: 

Do đó B'F = EF = DE ⇒ EF = DB'/3 .

Xét tam giác BCD vuông tại C, có:

BD² = BC² + CD² = a² + a² = 2a²

Xét tam giác B'BD vuông tại B, có:

B'D² = B'B² + BD² = a² + 2a² = 3a²

Vậy d((D'AC), (BC'A')) =