Bài 7.17 SGK Toán 11 Tập 2 Kết nối tri thức

Bài 7.17 SGK Toán 11 Tập 2 Kết nối tri thức:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.

a) Tính độ dài đường chéo của hình lập phương.

b) Chứng minh rằng (ACC'A') ⊥ (BDD'B').

c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng ∠COC' là một góc phẳng của góc nhị diện [C, BD, C']. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C'], [A, BD,C'].

Giải bài 7.17 SGK Toán 11 Tập 2 Kết nối tri thức:

Ta có hình vẽ minh hoạ sau:

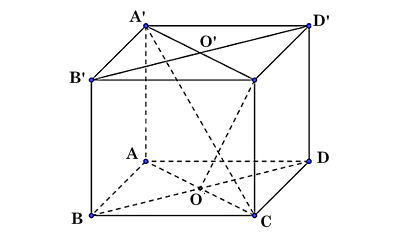
a) Vì ABCD.A'B'C'D' là hình lập phương nên có các mặt là hình vuông.

Xét tam giác ABC vuông tại B, có:

Vì AA' ⊥ (ABCD) nên AA' ⊥ AC.

Xét tam giác A'AC vuông tại A, có:

Vậy đường chéo của hình lập phương có độ dài là 

b) Vì AA' ⊥ (ABCD) nên AA' ⊥ BD.

Vì ABCD là hình vuông nên AC ⊥ BD mà AA' ⊥ BD, suy ra BD ⊥ (ACC'A').

Vì BD ⊥ (ACC'A') nên (ACC'A') ⊥ (BDD'B').

c) Vì BD ⊥ (ACC'A') nên BD ⊥ C'O mà CO ⊥ BD (do AC ⊥ BD)

nên  là góc phẳng nhị diện của góc nhị diện [C, BD, C'].

Do ABCD là hình vuông nên O là trung điểm của AC,

Suy ra: 

Xét ΔC'CO vuông tại C, có :

Vậy số đo của các góc nhị diện [C, BD, C'] khoảng 55°.

Vì AO ⊥ BD (do AC ⊥ BD), BD ⊥ C'O nên  là góc phẳng nhị diện của góc nhị diện [A, BD,C'].

Vì 

Vậy số đo góc nhị diện [A, BD,C'] khoảng 125°.