Bài 7.16 trang 47 Toán 10 tập 2 Kết nối tri thức

Bài 7.16 trang 47 Toán 10 Tập 2 Kết nối tri thức:

Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó.

Giải bài 7.16 trang 47 Toán 10 Tập 2 Kết nối tri thức:

Đường tròn ngoại tiếp tam giác ABC là đường tròn đi qua ba điểm A, B, C. 

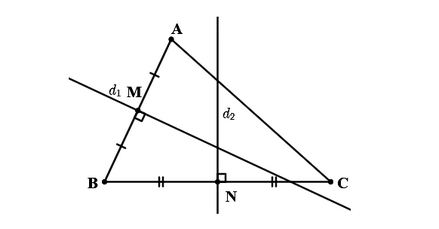
Các đoạn thẳng AB, BC tương ứng có trung điểm là M(5; 0), N(9/2; -3/2)

Đường thẳng trung trực d₁ của đoạn thẳng AB đi qua điểm M(5; 0) và có vectơ pháp tuyến 

Vì  cùng phương với  nên d₁ cũng nhận  là vectơ pháp tuyến.

Vi vậy, phương trình của d₁ là: 1(x – 5) – 2(y – 0) = 0

⇔ x – 2y – 5 = 0. 

Đường thẳng trung trực d₂ của đoạn thẳng BC đi qua N(9/2; -3/2) và có vectơ pháp tuyến

Nên phương trình d₂ là: 

⇔ x – 7y – 15 = 0. 

Tâm I của đường tròn (C) ngoại tiếp tam giác ABC cách đều ba điểm A, B, C nên I là giao điểm của d₁ và d₂. 

Vậy tọa độ của I là nghiệm của hệ phương trình:

Suy ra I(1; – 2). Đường tròn (C) có bán kính là:

Vậy phương trình của (C) là: (x – 1)² + (y + 2)² = 25.