Bài 9.21 trang 89 Toán 10 tập 2 Kết nối tri thức

Bài 9.21 trang 89 Toán 10 Tập 2 Kết nối tri thức:

Gieo một đồng xu cân đối liên tiếp bốn lần.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu.

b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.

Phân tích và Phương pháp giải

Xác định quy mô không gian mẫu

Mỗi lần gieo đồng xu có 2 kết quả (Sấp - S; Ngửa - N). Khi gieo 4 lần liên tiếp, tổng số kết quả của không gian mẫu theo quy tắc nhân là:

Chiến lược liệt kê biến cố

Để tìm biến cố có "2 sấp và 2 ngửa", chúng ta sẽ rà soát từng nhánh của sơ đồ hình cây. Một mẹo nhỏ là liệt kê theo thứ tự để tránh trùng lặp:

1. Các trường hợp bắt đầu bằng SS...

2. Các trường hợp bắt đầu bằng SN...

3. Các trường hợp bắt đầu bằng NS...

4. Các trường hợp bắt đầu bằng NN...

Giải bài 9.21 trang 89 Toán 10 Tập 2 Kết nối tri thức:

a) Đồng xu cân đối nên các kết quả có thể là đồng khả năng.

Kí hiệu S và N tương ứng là đồng xu ra mặt sấp và đồng xu ra mặt ngửa.

Theo bài ra ta có sơ đồ hình cây mô tả không gian mẫu như sau: 

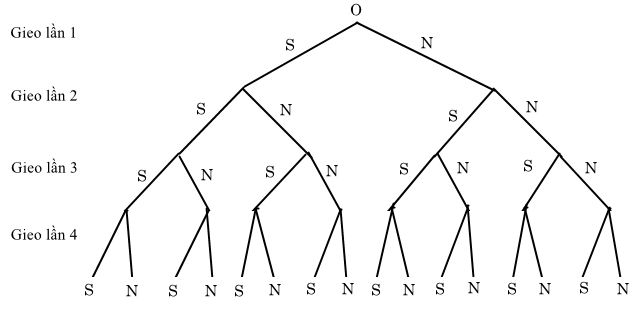
⇒ n(Ω) = 16.

b) Gọi biến cố A: “Trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”.

Theo sơ đồ hình cây ở câu a, ta có: 

A = {SSNN; SNSN; SNNS; NSSN; NSNS; NNSS}.

⇒  n(A) = 6. 

Vậy $P(G)=\frac{n(G)}{n(\Omega )}=\frac{6}{16}=\frac{3}{8}$