Bài 6 trang 22 Toán 8 Tập 2 Chân trời sáng tạo

Bài 6 trang 22 Toán 8 Tập 2 Chân trời sáng tạo: 

Một người đi bộ trên đường thẳng với tốc độ v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ)

a) Lập công thức tính s theo t

b) vẽ đồ thị của hàm số s theo biến số t khi v = 4

Giải bài 6 trang 22 Toán 8 Tập 2 Chân trời sáng tạo:

a) Lập công thức tính s theo t

 s = vt.

b) vẽ đồ thị của hàm số s theo biến số t khi v = 4

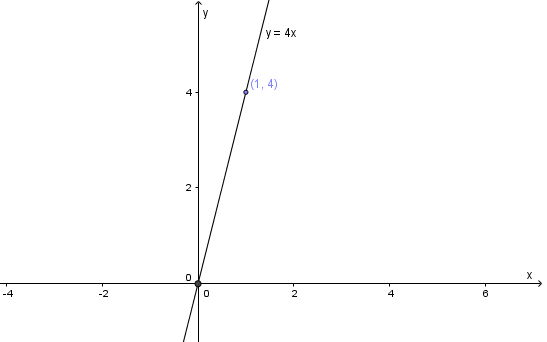
Hàm số: s = 4t.

Đồ thị hàm số s = 4t là đường thẳng đi qua 2 điểm O(0; 0); A(1; 4).