Bài 6 trang 18 Toán 9 tập 1 Cánh Diều

Đề bài:

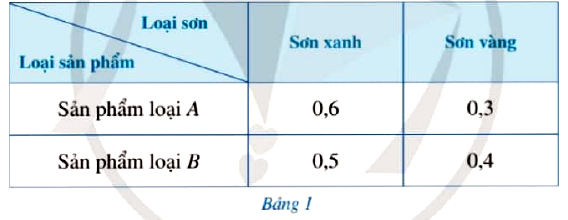
Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 1 (đơn vị: kg/1 sản phẩm).

Người ta dự định sử dụng 85 kg sơn xanh và 50 kg sơn vàng để sơn tất cả các sản phẩm của 2 loại đó. Gọi x, y lần lượt là số sản phẩm loại A, số sản phẩm loại B được sơn.

a) Viết hệ phương trình bậc nhất hai ẩn x, y.

b) Cặp số (100; 50) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, các em cần thực hiện các bước sau:

• Đối với câu a):

  • Dựa vào tổng lượng sơn xanh đã sử dụng để lập phương trình thứ nhất.

  • Dựa vào tổng lượng sơn vàng đã sử dụng để lập phương trình thứ hai.

  • Kết hợp hai phương trình đó để tạo thành một hệ phương trình.

• Đối với câu b):

  • Để kiểm tra một cặp số có phải là nghiệm của hệ phương trình hay không, ta thay giá trị của $x$ và $y$ vào từng phương trình trong hệ.

  • Nếu cặp số đó thỏa mãn tất cả các phương trình trong hệ, thì nó là nghiệm. Ngược lại, nếu nó không thỏa mãn dù chỉ một phương trình, nó không phải là nghiệm.

Lời giải chi tiết:

a) Viết hệ phương trình bậc nhất hai ẩn x, y.

Gọi x, y lần lượt là số sản phẩm loại A, số sản phẩm loại B được sơn.

Sử dụng 85kg sơn Xanh để sơn hai loại sản phẩm A, B, nên ta có:

0,6x + 0,5y = 85

Sử dụng 50kg sơn Vàng để sơn hai loại sản phẩm A, B, nên ta có:

03x + 0,4y = 50

Vậy x, y là nghiệm của hệ phương trình: 

b) Cặp số (100; 50) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Thay x = 100 và y = 50 vào từng phương trình của hệ, ta có:

0,6.100 + 0,5.50 = 85

0,3.100 + 0,4.50 = 50

Vậy cặp số (100; 50) là nghiệm của hệ phương trình ở câu a).