Giải bài 2 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)

Đề bài:

Một nhà máy sản xuất hai loại thuốc trừ sâu nông nghiệp là A và B. Cứ sản xuất mỗi thùng loại A thì nhà máy thải ra 0,25 kg khí cacbon dioxide (CO₂) và 0,60 kg khí sulffur dioxide (SO₂), sản xuất mỗi thùng loại B thì thải ra 0,50 kg CO₂  và  0,20 kg SO₂. Biết rằng, quy định hạn chế sản lượng (CO₂) của nhà máy tối đa là 75 kg và SO₂ tối đa là 90 kg mỗi ngày.

a) Tìm hệ bất phương trình mô tả số thùng của mỗi loại thuốc trừ sâu mà nhà máy có thể sản xuất mỗi ngày để đáp ứng các điều kiện hạn chế trên. Biểu diễn miền nghiệm của hệ bất phương trình đó trên mặt phẳng tọa độ.

b) Việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày có phù hợp với quy định không?

c) Việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày có phù hợp với quy định không?

Phân tích và Hướng dẫn giải:

Bài toán yêu cầu tìm số thùng thuốc trừ sâu loại A và B mà nhà máy có thể sản xuất mỗi ngày, với các điều kiện ràng buộc về lượng khí thải. Để giải quyết bài toán này, chúng ta sẽ thực hiện các bước sau:

a) Lập hệ bất phương trình: Gọi $x$ và $y$ là số thùng thuốc trừ sâu loại A và B. Dựa vào các điều kiện về lượng khí thải CO₂​ và SO₂​, chúng ta sẽ lập các bất phương trình tương ứng. Sau đó, biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ.

b) Kiểm tra tính phù hợp: Ta thay số lượng thùng của mỗi loại sản phẩm vào hệ bất phương trình đã lập. Nếu tất cả các bất phương trình đều thỏa mãn, phương án đó là phù hợp.

c) Kiểm tra tính phù hợp: Tương tự như câu b), ta thay các giá trị mới vào hệ bất phương trình để kiểm tra.

Lời giải chi tiết:

a) Gọi x (thùng) là số thùng thuốc trừ sâu loại A được sản xuất ra trong một ngày, y (thùng) là số thùng thuốc trừ sâu loại B nhà máy sản xuất ra trong một ngày.

- Hiển nhiên, ta có : x ≥ 0, y ≥ 0 và x,y ∈ N.

Khi đó, số khí CO_2, SO2 thải ra khi sản xuất x thùng thuốc trừ sâu loại A lần lượt là: 0,25x (kg) và 0,6x (kg).

Số khí CO_2, SO₂  thải ra khi sản xuất y thùng thuốc trừ sâu loại B lần lượt là: 0,5y (kg) và 0,2y (kg).

Tổng lượng khí CO₂ thải ra trong một ngày khi sản xuất x thùng thuốc loại A và y thùng thuốc loại B là: 0,25x + 0,5y (kg)

Tổng lượng khí SO₂ thải ra trong một ngày khi sản xuất x thùng thuốc loại A và y thùng thuốc loại B là: 0,6x + 0,2y (kg)

- Do quy định hạn chế sản lượng CO₂ của nhà máy tối đa là 75 kg và SO₂ tối đa là 90 kg mỗi ngày nên ta có các bất phương trình sau :

0,25x + 0,5y ≤ 75;

0,6x + 0,2y ≤ 90.

Vậy, ta có hệ bất phương trình trình mô tả số thùng của mỗi loại thuốc trừ sâu mà nhà máy có thể sản xuất mỗi ngày để đáp ứng các điều kiện hạn chế trên là:

Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ Oxy ta được hình sau:

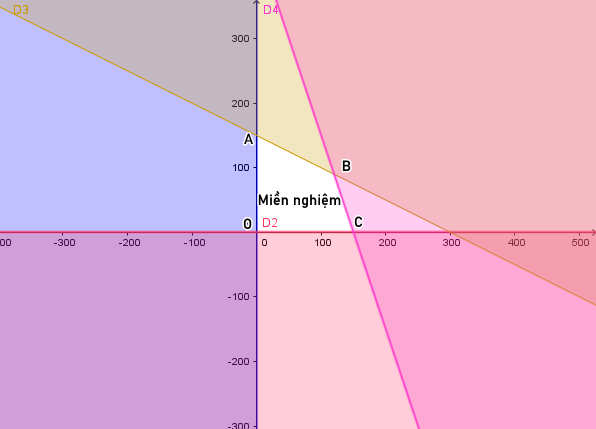
Vậy, miền màu trắng (không tô màu, miền tứ giác OABC bao gồm cả các cạnh) là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

b) Việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày tương ứng với x = 100 và y = 80.

Ta có, x = 100 và y = 80 thì:

Do đó, cặp (100; 80) là nghiệm của hệ bất phương trình.

Vậy, việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày là phù hợp với quy định.

c) Việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày tương ứng với x = 60 và y = 160.

Ta có, x = 60 và y = 160 thì:

Do đó, cặp (60; 160) không là nghiệm của hệ bất phương trình.

Việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày không phù hợp với quy định.