Giải bài 1.25 trang 21 Toán 10 Tập 1 SGK Kết nối tri thức: Các phép toán tập hợp

Đề bài:

Cho hai tập hợp A = [-2; 3] và B = (1; +∞). Xác định các tập hợp sau: A ∩ B; B \ A; C_ℝB.

Phân tích và Hướng dẫn giải

Để xác định các tập hợp kết quả, chúng ta nên biểu diễn các tập hợp $A$ và $B$ trên một trục số.

• Tập hợp A: Là đoạn từ -2 đến 3, bao gồm cả hai đầu mút.

• Tập hợp B: Là khoảng từ 1 đến $+\infty$, không bao gồm điểm 1.

Sau khi biểu diễn, ta áp dụng định nghĩa các phép toán trên tập hợp:

• Giao của hai tập hợp ($A\cap B$): Gồm các phần tử chung của cả A và B.

• Hiệu của hai tập hợp ($B\setminus A$): Gồm các phần tử thuộc B nhưng không thuộc A.

• Phần bù (C_R​B): Gồm các phần tử thuộc tập hợp số thực $\mathbb{R}$ nhưng không thuộc B.

Lời giải chi tiết bài 1.25 trang 21 Toán 10:

Ta biểu diễn các tập trên trục số như sau:

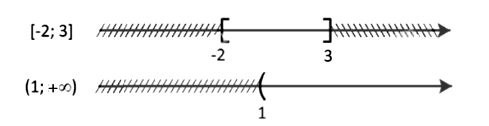
Do đó, ta có:

• Giao của hai tập hợp A và B là:

A ∩ B = [–2; 3] ∩ (1; +∞) = (1; 3].

• Hiệu của B và A là:

B \ A = (1; +∞) \ [–2; 3] = (3; +∞).

• Phần bù của B trong ℝ là:

C_ℝB = ℝ \ B = ℝ \ (1; +∞) = (–∞; 1].