Giải 1.9 Toán 9 tập 1 SGK Kết nối tri thức
Chào các em! Hôm nay chúng ta sẽ cùng giải chi tiết Bài 1.9 trang 16 trong sách giáo khoa Toán 9 tập 1, bộ sách Kết nối tri thức với cuộc sống. Bài toán này sẽ giúp các em làm quen với việc sử dụng máy tính cầm tay (MTCT) để tìm nghiệm của các hệ phương trình bậc nhất hai ẩn, một công cụ hữu ích để kiểm tra kết quả hoặc giải nhanh bài tập.
Đề bài:
Dùng MTCT thích hợp để tìm nghiệm của các hệ phương trình sau:
a)
b)
c)
d)
Phân tích và Hướng dẫn giải
Hầu hết các loại máy tính cầm tay phổ biến (như Casio fx-570VN PLUS, fx-880BTG,...) đều có chức năng giải hệ phương trình. Để sử dụng hiệu quả, các em cần thực hiện theo các bước sau:
-
Chuyển đổi hệ phương trình: Đưa hệ phương trình về dạng chuẩn:
Điều này rất quan trọng, đặc biệt với những phương trình chưa được sắp xếp đúng thứ tự.
-
Vào chế độ giải hệ phương trình: Thường là chế độ "EQN" hoặc "System of Equations" trong menu của máy tính.
-
Nhập các hệ số: Nhập lần lượt các hệ số
vào máy tính.
-
Đọc kết quả: Bấm phím "=" để máy tính hiển thị nghiệm
và
. Máy tính cũng sẽ thông báo nếu hệ phương trình có vô số nghiệm hoặc vô nghiệm.
Lời giải chi tiết:
a)
-
Xác định hệ số: a1=12, b1=−5, c1=−24; a2=−5, b2=−3, c2=10.
-
Sử dụng máy tính: Nhập các hệ số vào máy tính.
-
Kết quả:
-
x = −2
-
y = 0
-
Vậy, nghiệm của hệ phương trình là (−2;0).
-
b)
-
Xác định hệ số: a1=1/3, b1=−1, c1=2/3; a2=1, b2=−3, c2=2.
-
Sử dụng máy tính: Nhập các hệ số vào máy tính.
-
Kết quả:
-
Máy tính báo "Many Solutions" (Vô số nghiệm).
-
Vậy, hệ phương trình đã cho có vô số nghiệm.
-
c)
-
Xác định hệ số: a1=3, b1=−2, c1=1; a2=-1, b2=2/3, c2=0.
-
Sử dụng máy tính: Nhập các hệ số vào máy tính.
-
Kết quả:
-
Máy tính báo "No Solution" (Vô nghiệm).
-
Vậy, hệ phương trình đã cho vô nghiệm.
-
d)
-
Xác định hệ số: a1=4/9, b1=−3/5, c1=11; a2=2/9, b2=1/5, c2=-2.
-
Sử dụng máy tính: Nhập các hệ số vào máy tính.
-
Kết quả:
-
x = 9/2
-
y = −15
-
Vậy, nghiệm của hệ phương trình là (9/2;−15).
-
Qua bài tập này, các em đã làm quen với việc sử dụng máy tính cầm tay để giải hệ phương trình. Đây là một công cụ đắc lực giúp các em kiểm tra lại kết quả của mình một cách nhanh chóng. Tuy nhiên, hãy nhớ rằng việc nắm vững các phương pháp đại số (thế, cộng đại số) vẫn là quan trọng nhất để hiểu bản chất của bài toán.
» Xem thêm:
Bài 1.7 Toán 9 Tập 1 Kết nối tri thức: Giải các hệ phương trình sau bằng phương pháp cộng đại số: a) 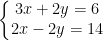 ...
...
Bài 1.8 Toán 9 Tập 1 Kết nối tri thức: Cho hệ phương trình &space;\end{matrix}\right.) , trong đo m là số đã cho. Giải hệ...
, trong đo m là số đã cho. Giải hệ...
Bài 1.10 Toán 9 Tập 1 Kết nối tri thức: Cho hai phương trình: -2x + 5y = 7 (1)...
Bài 1.11 Toán 9 Tập 1 Kết nối tri thức: Giải các hệ phương trình sau bằng phương pháp thế:...
Đánh giá & nhận xét
-
 Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.23 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.23 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.27 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.27 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.26 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.26 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.25 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.25 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.24 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.24 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.23 Toán 9 tập 1 SGK Kết nối tri thức
Bài 3.23 Toán 9 tập 1 SGK Kết nối tri thức
-
 Bài 3.22 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.22 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.21 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.21 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.20 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.20 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.19 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.19 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.18 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.18 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.17 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.17 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.16 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.16 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.15 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.15 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.14 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.14 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.13 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.13 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.12 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.12 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.11 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.11 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.10 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.10 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.9 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.9 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.8 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.8 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.7 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.7 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.6 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.6 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.5 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.5 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.4 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.4 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.3 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.3 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.2 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.2 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.1 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.1 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.20 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.20 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.19 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.19 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.18 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.18 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.17 trang 41 Toán 9 tập 1 Kết nối tri thức: Bất Phương Trình Bậc Nhất Một Ẩn
Bài 2.17 trang 41 Toán 9 tập 1 Kết nối tri thức: Bất Phương Trình Bậc Nhất Một Ẩn


















































