Giải 1.7 Toán 9 tập 1 SGK Kết nối tri thức
Chào các em! Hôm nay, chúng ta sẽ cùng giải chi tiết Bài 1.7 trang 16 trong sách giáo khoa Toán 9 tập 1, bộ sách Kết nối tri thức với cuộc sống. Bài toán này sẽ giúp các em củng cố và làm quen với phương pháp cộng đại số để giải hệ phương trình bậc nhất hai ẩn.
Đề bài:
Giải các hệ phương trình sau bằng phương pháp cộng đại số
a)
b)
c)
Phân tích và Hướng dẫn giải
Phương pháp cộng đại số là một kỹ thuật mạnh mẽ để giải hệ phương trình. Các bước thực hiện như sau:
-
Nhân các phương trình với một số thích hợp: Mục tiêu là làm cho hệ số của một trong hai ẩn (ví dụ: x hoặc y) trong hai phương trình trở thành đối nhau hoặc bằng nhau.
-
Cộng hoặc trừ hai phương trình:
-
Nếu hệ số của một ẩn là đối nhau, ta cộng hai phương trình lại với nhau.
-
Nếu hệ số của một ẩn là bằng nhau, ta trừ hai phương trình cho nhau.
-
Khi đó, một ẩn sẽ bị triệt tiêu, và ta thu được một phương trình mới chỉ chứa một ẩn.
-
-
Giải phương trình một ẩn: Giải phương trình mới để tìm giá trị của ẩn đó.
-
Tìm ẩn còn lại: Thay giá trị vừa tìm được vào một trong hai phương trình ban đầu để tìm giá trị của ẩn còn lại.
-
Kết luận: Cặp số (x;y) tìm được chính là nghiệm của hệ phương trình.
Lời giải chi tiết:
a)
(cộng từng vế pt thứ nhất với pt thứ hai)
Vậy nghiệm của hệ phương trình đã cho là (4; –3)
b)
(Nhân hai vế của pt thức nhất với 4)
(Cộng từng vế pt thứ nhất với pt thứ hai)
Vậy nghiệm của hệ pt đã cho là (5; 3)
c)
(Nhân từng vế pt thứ nhất với 3 pt thứ hai với 2)
(Cộng từng vế pt thứ nhất với pt thứ hai)
pt thứ hai ta có: x = 3y – 4
Ta thấy hệ có vô số nghiệm
Nghiệm của hệ đã cho là: (3y – 4; y) với mọi y thuộc R.
Qua bài tập này, các em đã rèn luyện được cách giải hệ phương trình bằng phương pháp cộng đại số. Hãy nhớ rằng, phương pháp này rất hiệu quả khi các hệ số của một ẩn dễ dàng làm cho bằng hoặc đối nhau.
» Xem thêm:
Bài 1.6 Toán 9 Tập 1 Kết nối tri thức: Giải các hệ phương trình sau bằng phương pháp thế: a) 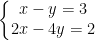 ...
...
Bài 1.8 Toán 9 Tập 1 Kết nối tri thức: Cho hệ phương trình &space;\end{matrix}\right.) , trong đo m là số đã cho. Giải hệ...
, trong đo m là số đã cho. Giải hệ...
Bài 1.9 Toán 9 Tập 1 Kết nối tri thức: Dùng MTCT thích hợp để tìm nghiệm của các hệ phương trình sau: a) 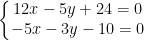 ...
...
Đánh giá & nhận xét
-
 Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.23 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.23 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.27 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.27 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.26 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.26 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.25 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.25 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.24 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.24 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.23 Toán 9 tập 1 SGK Kết nối tri thức
Bài 3.23 Toán 9 tập 1 SGK Kết nối tri thức
-
 Bài 3.22 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.22 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.21 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.21 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.20 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.20 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.19 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.19 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.18 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.18 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.17 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.17 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.16 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.16 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.15 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.15 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.14 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.14 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.13 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.13 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.12 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.12 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.11 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.11 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.10 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.10 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.9 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.9 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.8 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.8 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.7 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.7 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.6 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.6 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.5 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.5 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.4 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.4 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.3 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.3 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.2 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.2 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.1 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.1 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.20 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.20 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.19 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.19 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.18 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.18 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.17 trang 41 Toán 9 tập 1 Kết nối tri thức: Bất Phương Trình Bậc Nhất Một Ẩn
Bài 2.17 trang 41 Toán 9 tập 1 Kết nối tri thức: Bất Phương Trình Bậc Nhất Một Ẩn


















































