Bài 4 trang 65 Toán 8 Tập 2 Cánh Diều

Bài 4 trang 65 Toán 8 Cánh Diều Tập 2:

Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.

Giải Bài 4 trang 65 Toán 8 Cánh Diều Tập 2:

Ta có hình vẽ sau:

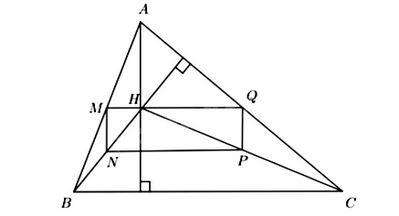
Vì M, N lần lượt là trung điểm của các đoạn thẳng AB, BH nên ta có:

MN là đường trung bình tam giác ABH  mà  nên  (1)

Vì P, Q lần lượt là trung điểm của các đoạn thẳng CH, AC nên ta có:

PQ là đường trung bình tam giác AHC  mà  nên  (2)

Vì P, N lần lượt là trung điểm của các đoạn thẳng CH, BH nên ta có:

PN là đường trung bình tam giác BHC  mà  nên (3)

Vì M, Q lần lượt là trung điểm của các đoạn thẳng AB, AC nên ta có:

MQ là đường trung bình tam giác ABC  mà  nên (4)

Từ (1), (2), (3), (4) ta có 

Vậy tứ giác MNPQ là hình chữ nhật (đpcm).