Bài 3 trang 14 Toán 8 Tập 2 Chân trời sáng tạo: Hệ Trục Tọa Độ Oxy & Hình Học

Đề bài

Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm A(–3 ; 3), B(3 ; 3), C(3 ; –3), D(–3 ; –3). Tứ giác ABCD là hình gì? 

Phân tích kiến thức và hướng dẫn giải chi tiết

1. Phương pháp giải

Để xác định hình dạng của tứ giác $ABCD$, ta có thể dựa vào tọa độ của các đỉnh để tính toán độ dài các cạnh và kiểm tra các tính chất đặc trưng của hình (ví dụ: các cạnh bằng nhau, các góc vuông, các đường chéo bằng nhau và vuông góc).

2. Lời giải chi tiết bài 3 trang 14 Toán 8

• Bước 1: Xác định vị trí các điểm

  • Điểm A(-3; 3): Nằm ở góc phần tư thứ hai.

  • Điểm B(3; 3): Nằm ở góc phần tư thứ nhất.

  • Điểm C(3; -3): Nằm ở góc phần tư thứ tư.

  • Điểm D(-3; -3): Nằm ở góc phần tư thứ ba.

• Bước 2: Tính độ dài các cạnh

  Sử dụng công thức tính khoảng cách giữa hai điểm trong mặt phẳng tọa độ: .

  • 

  • 

  • 

  • 

• Bước 3: Nhận xét

  • Ta thấy các cạnh AB = BC = CD = DA = 6. Tứ giác ABCD có bốn cạnh bằng nhau, nên nó là hình thoi.

  • Kiểm tra thêm các góc: Cạnh AB song song với trục hoành, cạnh BC song song với trục tung. Do đó, , suy ra góc B là góc vuông.

  • Một hình thoi có một góc vuông là hình vuông.

Tổng kết và lời khuyên

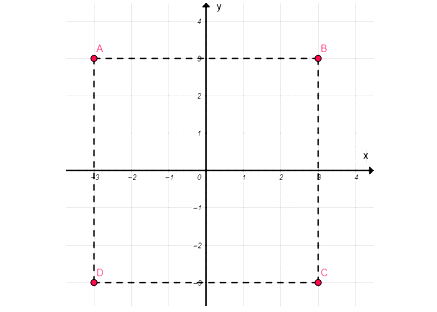
Đáp số: Tứ giác ABCD là hình vuông.