Bài 2.3 SGK Toán 12 tập 1 Kết nối tri thức: Ứng Dụng Vectơ Trong Vật Lí

Đề bài

Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ  phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ ). 

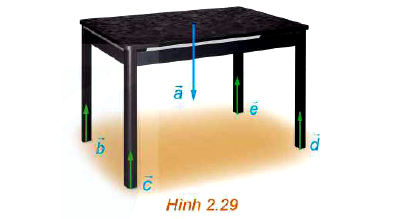
a) Hãy chỉ ra mối quan hệ về phương và hướng của các vectơ  và .

b) Giải thích vì sao các vectơ  đôi một bằng nhau.

Phân tích kiến thức và hướng dẫn giải chi tiết

1. Các khái niệm cần nhớ

• Vectơ: Một đại lượng có hướng, được xác định bởi phương, hướng và độ lớn.

• Phương: Thể hiện bởi đường thẳng chứa vectơ.

• Hướng: Thể hiện bởi chiều của mũi tên.

• Độ lớn: Thể hiện bởi độ dài của vectơ.

2. Lời giải chi tiết bài 2.3 trang 58 Toán 12

a) Mối quan hệ về phương và hướng

• Về phương:

  Trọng lực  có phương thẳng đứng (vuông góc với mặt sàn). Các phản lực từ mặt sàn  cũng có phương thẳng đứng.

  Vậy, các vectơ  cùng phương với nhau.

• Về hướng:

  Trọng lực  có hướng từ trên xuống dưới.

  Các phản lực từ mặt sàn có hướng từ dưới lên trên.

  Vậy, các vectơ  cùng hướng với nhau, nhưng ngược hướng với vectơ .

b) Giải thích sự bằng nhau của các vectơ

• Về độ lớn:

  • Vì chiếc bàn cân đối và trọng lực  được phân tán đều qua bốn chân bàn, nên độ lớn của các phản lực tại mỗi chân bàn bằng nhau.

  • .

• Về sự bằng nhau của vectơ:

  • Hai vectơ được gọi là bằng nhau nếu chúng cùng phương, cùng hướng và có cùng độ lớn.

  • Các vectơ  đều có cùng phương (thẳng đứng), cùng hướng (từ dưới lên) và có cùng độ lớn.

  • Vậy, các vectơ  đôi một bằng nhau.

Tổng kết và lời khuyên

Đáp số:

a) Các vectơ  cùng phương;  cùng hướng với nhau nhưng ngược hướng với $\vec{a}$.

b) Vì các vectơ  cùng phương, cùng hướng và có cùng độ lớn nên chúng đôi một bằng nhau.