Bài 1.29 SGK Toán 12 tập 1 Kết nối tri thức

Đề bài 1.29 - SGK Toán 12 Tập 1 Kết nối tri thức:

Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức:

Trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.

a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số x = x(p). Từ đồ thị đã vẽ, hãy cho biết:

- Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;

- Ý nghĩa thực tiễn của giới hạn 

Hướng dẫn giải chi tiết bài 1.29 SGK Toán 12 Tập 1:

a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.

Ta có: 

Tập xác định của hàm số là: (0; 354]

Với p = 240, ta có: 

Vậy với giá bán mỗi đơn vị sản phẩm là 240 nghìn đồng thì bán được 47,5 đơn vị sản phẩm.

b) Khảo sát sự biến thiên của hàm số:

 với mọi p ∈ (0; 354]

Hàm số không có cực trị.

Giới hạn: 

Nên p = 0 là tiệm cận đứng

Bảng biến thiên:

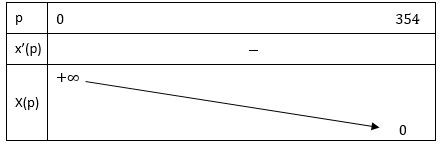
3. Đồ thị

Ta có: x(p) = 0 ⇔ p = 354

Đò thị hàm số x(p) cắt trục hoành tại điểm (354; 0); đi qua các điểm (300; 18); (200; 77)

Đồ thị x(p) với p ∈ (0; 354] là phần đường màu tím như hình sau:

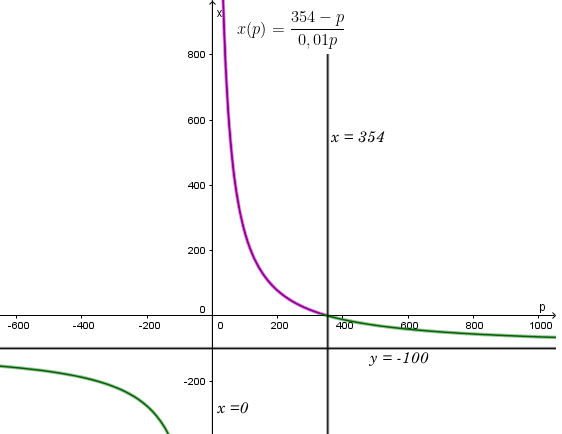
- Số lượng đơn vị sản phẩm bán sẽ giảm đi khi giá bán tăng, và sẽ không bán được sản phẩm nào nếu giá bán là 354 nghìn đồng

- Ý nghĩa thực tiễn của giới hạn : Vì nên giá bán càng thấp thì số lượng đơn vị sản phẩm sẽ bán được càng nhiều.