Giải biện luận hệ phương trình bậc nhất 2 ẩn theo tham số m và Bài tập vận dụng - Toán 9 chuyên đề

11:22:4330/08/2022

Giải biện luận hệ phương trình bậc nhất 2 ẩn theo tham số m là một dạng toán mang tính khái quát cao. Việc giải những bài tập mang tính khái quát này đòi hỏi các em nắm vững kiến thức lý thuyết.

Vậy cách giải biện luận hệ phương trình bậc nhất 2 ẩn theo tham số m hay cách tìm m để hệ phương trình bậc nhất có nghiệm duy nhất, vô nghiệm hay có vô số nghiệm như thế nào? chúng ta sẽ tìm hiểu qua bài viết dưới đây và vận dụng giải một số bài tập minh hoạ.

» Đừng bỏ lỡ: Cách giải hệ phương trình có chứa tham số m cực hay

I. Cách giải và biện luận hệ phương trình bậc nhất 2 ẩn theo tham số m

Để giải Bài tập biện luận phương trình bậc nhất 2 ẩn hay một số dạng bài tập tương tự như tìm m để hệ phương trình bậc nhất 2 ẩn có nghiệm duy nhất, vô nghiệm, vô số nghiệm chúng ta thực hiện các bước sau:

+ Bước 1: Đựa hệ phương trình về phương trình dạng bậc nhất dạng ax + b = 0. (sử dụng phương pháp thế, phương pháp cộng đại số,...)

+ Bước 2: Xét phương trình bậc nhất: ax + b = 0, (với a, b là hằng số) (*).

- TH1: Nếu a ≠ 0 thì phương trình (*) có nghiệm duy nhất x = -b/a. từ đó tìm được y.

- TH2: Nếu a = 0, b ≠ 0 thì phương trình (*) vô nghiệm.

- TH3: Nếu a = 0, b = 0 thì phương trình (*) có vô số nghiệm.

+ Bước 3: Kết luận nghiệm của hệ phương trình.

* Lưu ý: Đối với dạng bài tập biện luận hệ phương trình bậc nhất 2 ẩn chúng ta thường sử dụng phương pháp thế.

hayhochoi vn

II. Bài tập giải biện luận phương trình bậc nhất 2 ẩn, tìm m để hệ phương trình có nghiệm duy nhất, vô nghiệm, vô số nghiệm

* Bài tập 1: Cho hệ phương trình:

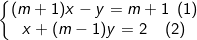
$\small \left\{\begin{matrix} (m+1)x-y=m+1\: \: (1)\\ x+(m-1)y=2 \: \:\: \: \: (2)\end{matrix}\right.$

Giải và biện luận hệ phương trình bậc nhất 2 ẩn trên theo tham số m.

* Lời giải:

- Từ PT (1) của hệ ta có:

y = (m + 1)x - (m + 1); (3)

thế vào PT 2) ta được:

x + (m - 1)[(m + 1)x - (m + 1)] = 2

⇔ x + (m² - 1)x - (m² - 1) = 2

⇔ m²x = m² + 1. (4).

- TH1: Nếu m ≠ 0 thì PT (4) có nghiệm duy nhất:

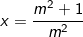$\small x=\frac{m^2+1}{m^2}$ thay vào (3) ta có:

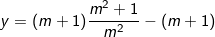
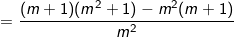
$\small y=(m+1)\frac{m^2+1}{m^2}-(m+1)$ $\small =\frac{(m+1)(m^2+1)-m^2(m+1)}{m^2}$

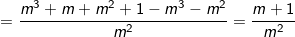
$\small =\frac{m^3+m+m^2+1-m^3-m^2}{m^2}=\frac{m+1}{m^2}$

⇒ Hệ phương trình có nghiệm duy nhất:

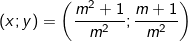
$\small (x;y)=\left (\frac{m^2+1}{m^2};\frac{m+1}{m^2} \right )$

- TH2: Nếu m = 0 thì PT (4) trở thành 0x = 1 nên vô nghiệm.

⇒ Hệ phương trình đã cho vô nghiệm.

- Kết luận:

Với m ≠ 0 hệ phương trình có nghiệm duy nhất:

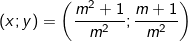$\small (x;y)=\left (\frac{m^2+1}{m^2};\frac{m+1}{m^2} \right )$ .

Với m = 0 hệ phương trình đã cho vô nghiệm.

* Bài tập 2: Cho hệ phương trình bậc nhất 2 ẩn:

$\small \left\{\begin{matrix} mx+3y=-2\\ m^2x-6y=4 \end{matrix}\right.$

a) Tìm giá trị m để hệ phương trình có nghiệm duy nhất;

b) Tìm giá trị m để hệ phương trình có vô số nghiệm.

* Lời giải:

- Xét phương trình (1) của hệ: mx + 3y = -2, ta được:

$\small y=\frac{1}{3}(-mx-2)$ (3)

Thế y ở phương trình (3) vào phương trình (2) của hệ: m²x - 6y = 4, ta được

$\small m^2x-6.\frac{1}{3}(-mx-2)=4$

$\small \Leftrightarrow (m^2+2m)x=0$

a) Hệ có nghiệm duy nhất khi:

m² + 2m ≠ 0 ⇔ m ≠ 0 và m ≠ -2.

Khi đó hệ có nghiệm: x = 0 và y = -2/3.

b) Hệ có vô số nghiệm khi:

m² + 2m = 0 ⇔ m = 0 hoặc m = -2.

Vậy với m = 0 hoặc m = -2 hệ có vô số nghiệm

* Bài tập 3: Cho hệ phương trình bậc nhất 2 ẩn:

$\small \left\{\begin{matrix} x+y=1\\ mx+2y=m \end{matrix}\right.$

a) Tìm m để hệ phương trình có nghiệm duy nhất;

b) Tìm m để hệ phương trình có vô số nghiệm.

* Lời giải:

- Xét phương trình (1): x + y = 1 ta biến đổi được: y = 1 - x

Thay vào phương trình (2): mx + 2y = m, ta được:

mx + 2(1 - x) = m

⇔ (m - 2)x = m - 2 (*)

a) Hệ có nghiệm duy nhất khi

phương trình (*) có nghiệm duy nhất ⇔ m - 2 ≠ 0 ⇔ m ≠ 2

khi đó: x = 1 ⇒ y = 1 - 1 = 0

Tức hệ có nghiệm (x;y) = (1;0)

b) Hệ có vô số nghiệm khi:

phương trình (*) có vô số nghiệm ⇔ m - 2 = 0 ⇔ m = 2

Vậy m = 2 hệ có vô số nghiệm.

* Bài tập 4: Cho hệ phương trình bậc nhất 2 ẩn:

$\small \left\{\begin{matrix} x+my=1\\ mx-y=-m \end{matrix}\right.$ $\small \begin{matrix} (1)\\ (2) \end{matrix}$

a) Chứng tỏ rằng với mọi m hệ luôn có nghiệm duy nhất

b) Tìm giá trị của m để hệ có nghiệm (x,y) là một điểm thuộc gốc phần tư thứ I

* Lời giải:

a) Chứng tỏ rằng với mọi m hệ luôn có nghiệm duy nhất

Xét pt (2) của hệ, ta có: y = mx + m (3)

Thay (3) vào phương trình (1), ta được:

x + m(mx + m) = 1

⇔ (m² + 1)x = 1 - m²

$\small \Leftrightarrow x=\frac{1-m^2}{m^2+1}$

Thay vào (3), ta được:

$\small y=m.\frac{1-m^2}{m^2+1}+m$

$\small =\frac{m(1-m^2)+m(m^2+1)}{m^2+1}=\frac{2m}{m^2+1}$

Vậy với mọi m hệ luôn có nghiệm duy nhất.

b) Tìm giá trị của m để hệ có nghiệm (x,y) là một điểm thuộc gốc phần tư thứ I

Để (x, y) là một điểm thuộc góc phần tư thứ I, điều kiện là x > 0 và y > 0.

$\small \Leftrightarrow \left\{\begin{matrix} \frac{1-m^2}{m^2+1}>0\\ \frac{2m}{m^2+1}>0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 1-m^2>0\\ 2m>0 \end{matrix}\right.$

$\small \Leftrightarrow \left\{\begin{matrix} m^2<1\\ m>0 \end{matrix}\right.\Leftrightarrow 0<m<1$

Vậy với 0 < m < 1 thì hệ sẽ có 2 nghiệm (x,y) là một điểm thuộc gốc phần tư thứ I

* Bài tập 5: Cho hệ phương trình sau:

$\small \left\{\begin{matrix} x+my=11\\ 5x-3y=m+1 \end{matrix}\right.$

Tìm m để hệ phương trình có nghiệm

* Bài tập 6: Cho hệ phương trình sau:

$\small \left\{\begin{matrix} 3mx+5y=1\\ 2x+my=-4 \end{matrix}\right.$

Tìm m để hệ phương trình có nghiệm duy nhất.

* Bài tập 7: Cho hệ phương trình sau:

$\small \left\{\begin{matrix} x-3y=m\\ -5x+15y=-20 \end{matrix}\right.$

a) Tìm m để hệ phương trình có vô số nghiệm

b) Tìm m để hệ phương trình vô nghiệm

* Bài tập 8: Cho hệ phương trình:

$\small \left\{\begin{matrix} mx+2y=5\\ 2x+y=m \end{matrix}\right.$

a) Tìm m để hệ phương trình có nghiệm duy nhất.

b) Tìm m để hệ phương trình có vô số nghiệm

c) Tìm m để hệ phương trình vô nghiệm

Hy vọng với bài viết Giải biện luận hệ phương trình bậc nhất 2 ẩn theo tham số m và Bài tập vận dụng lớp 9 ở trên của Hay Học Hỏi giúp ích cho các em. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để $\small hayhochoi.vn$ ghi nhận và hỗ trợ, chúc các em học tốt.

Giải biện luận hệ phương trình bậc nhất 2 ẩn theo tham số m và Bài tập vận dụng - Toán 9 chuyên đề

Tags:

Đánh giá & nhận xét