Giải bài 5 trang 33 Toán 11 tập 1 SGK Chân trời sáng tạo

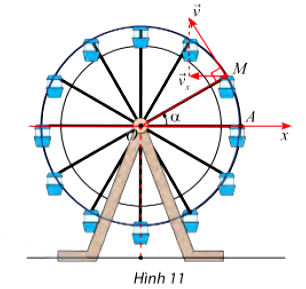
Bài 5 trang 33 Toán 11 tập 1 SGK Chân trời sáng tạo: Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác α = (Ox, OM) tho hàm số v_x = 0,3sinα (m/s) (hình 11).

a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của v_x

b) Dựa vào đồ thị của hàm số sin, hãy cho biết trong vòng quay đầu tiên (0 ≤ α ≤ 2π), góc α ở trong các khoảng nào thì v_x tăng.

Giải bài 5 trang 33 Toán 11 tập 1 SGK Chân trời sáng tạo:

a) Do -1 ≤ sinα ≤ 1 mà v_x = 0,3sinα

⇒ -0,3 ≤ v_x ≤ 0,3

Vậy giá trị lớn nhất của v_x là 0,3 (m) và giá trị nhỏ nhất của v_x là -0,3 (m).

b) Dựa vào đồ thị hàm số sin, ta thấy vòng quay đầu tiên (0 ≤ α ≤ 2π),

v_x tăng khi 0 ≤ α ≤ π/2 và 3π/2 ≤ α ≤ 2π