Giải bài 4.6 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức

Đề bài:

Cho Hình 4.20, biết AB = CB, AD = CD, 

a) Chứng minh rằng ΔABD = ΔCBD

b) Tính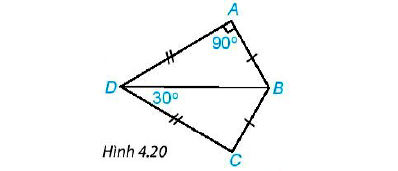 

Phân Tích và Hướng Dẫn Giải:

Để giải quyết bài toán này, các em cần áp dụng các kiến thức sau:

• Trường hợp bằng nhau c.c.c: Nếu ba cạnh của tam giác này bằng ba cạnh tương ứng của tam giác kia thì hai tam giác đó bằng nhau.

• Tính chất của hai tam giác bằng nhau: Các cặp cạnh và góc tương ứng của chúng bằng nhau.

• Tổng ba góc trong tam giác: Tổng ba góc trong một tam giác bằng 180^∘.

• Tính chất góc nhọn trong tam giác vuông: Trong tam giác vuông, hai góc nhọn phụ nhau (tổng bằng 90^∘).

Lời giải chi tiết:

a) Xét ΔABD và ΔCBD có:

AB = BC (theo giả thiết).

AD = CD (theo giả thiết).

BD chung.

⇒ ΔABD = ΔCBD (c-c-c)

b) Vì ΔABD = ΔCBD nên  (2 góc tương ứng)

Nên 

Xét ΔABD vuông tại A có:

  (trong tam giác vuông, hai góc nhọn phụ nhau).

Suy ra: 

Vì ΔABD = ΔCBD nên  (2 góc tương ứng)

Nên

Khi đó: 

Vậy