Giải bài 3.31 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức

Bài 3.31 trang 58 Toán 7 Tập 1 Kết nối tri thức:

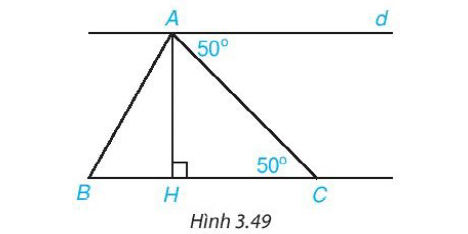
Cho Hình 3.49. Chứng minh rằng:

a) d // BC;

b) d ⊥ AH

c) Trong các kết luận trên, kết luận nào được suy ra từ tính chất của hai đường thẳng song song, kết luận nào được suy ra từ dấu hiệu nhận biết hai đường thẳng song song?

Giải bài 3.31 trang 58 Toán 7 Tập 1 Kết nối tri thức:

a) Ta có 

Mà hai góc này ở vị trí so le trong nên d // BC (đpcm)

b) Áp dụng định lí: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại” ta có:

Vì BC ⊥ AH, BC // d nên d ⊥ AH (đpcm)

c) Trong hai kết luận trên, kết luận d // BC được suy ra từ dấu hiệu nhận biết hai đường thẳng song song.

Kết luận d ⊥ AH được suy ra từ tính chất hai đường thẳng song song.