Giải bài 3.34 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Chào các em! Bài toán này là một ví dụ tuyệt vời về cách sử dụng các định lý hình học để chứng minh một công thức quan trọng về góc. Bằng cách kẻ thêm một đường thẳng phụ song song, chúng ta có thể dễ dàng giải quyết bài toán này một cách logic. Hãy cùng nhau khám phá nhé!
Đề bài:
Cho Hình 3.50, trong đó hai tia Ax, By nằm trên hai đường thẳng song song. Chứng minh rằng
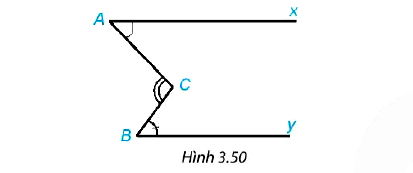
Phân Tích và Hướng Dẫn Giải:
Để chứng minh đẳng thức về góc này, chúng ta không thể làm trực tiếp. Thay vào đó, ta sẽ sử dụng một đường thẳng phụ. Cụ thể, chúng ta sẽ kẻ một tia Cz song song với Ax.
-
Sử dụng tính chất bắc cầu: Vì Ax//By và Cz//Ax, ta có thể suy ra Cz//By.
-
Áp dụng định lý về góc so le trong: Khi có các cặp đường thẳng song song, các góc so le trong sẽ bằng nhau.
-
Sử dụng tính chất cộng góc: Góc lớn ACB có thể được chia thành hai góc nhỏ hơn.
Giải bài 3.34 trang 59 Toán 7 Tập 1 Kết nối tri thức:
Kẻ tia Cz song song với Ax, nên Cz song song với By.
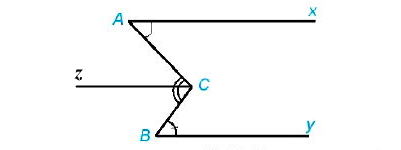
Vì Ax song song với Cz nên (2 góc so le trong).
Vì By song song với Cz nên (2 góc so le trong).
Khi đó
hay (đpcm)
Qua bài 3.34, các em đã rèn luyện được kỹ năng sử dụng đường thẳng phụ để giải quyết các bài toán chứng minh hình học. Việc nắm vững các định lý về góc so le trong, đồng vị và tính chất bắc cầu của đường thẳng song song là chìa khóa để giải quyết các bài toán phức tạp hơn. Chúc các em học tốt!
• Xem thêm:
Đánh giá & nhận xét
-
 Giải bài 4.11 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.11 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.10 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.10 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.9 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.9 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.8 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.8 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.7 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.7 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.6 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.6 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.5 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.5 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.4 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.4 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.3 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.3 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.2 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.2 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.1 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.1 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.36 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.36 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.35 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.35 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.33 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.33 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.32 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.32 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.31 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.31 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.30 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.30 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.29 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.29 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.28 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.28 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.27 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.27 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.26 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.26 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.25 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.25 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.24 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.24 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.23 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.23 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.22 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.22 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.21 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.21 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.20 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.20 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.19 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức: Đường thẳng song song
Giải bài 3.19 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức: Đường thẳng song song
-
 Giải bài 3.18 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.18 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.17 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.17 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.16 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
Giải bài 3.16 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
-
 Giải bài 3.15 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.15 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.14 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.14 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.13 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.13 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.12 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.12 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.11 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.11 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.10 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
Giải bài 3.10 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
-
 Giải bài 3.9 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.9 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.8 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.8 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức


















































