Hotline 0936685849

Giải bài 4.10 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức

09:50:1413/10/2023

Chào các em! Bài toán này là một ví dụ tuyệt vời về cách áp dụng các định lý hình học để tính số đo các góc còn thiếu. Bằng cách sử dụng định lý tổng ba góc của một tam giác và góc ngoài của tam giác, chúng ta có thể dễ dàng giải quyết bài toán này một cách chính xác. Hãy cùng nhau khám phá nhé!

Đề bài:

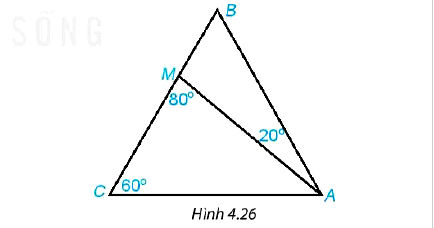
Cho tam giác ABC có $\small \widehat{BCA}=60^0$ và điểm M nằm trên cạnh BC sao cho $\small \widehat{BAM}=20^0;\: \: \widehat{AMC}=80^0$ (H.4.26). Tính số đo các góc AMB, ABC, BAC.

Bài 4.10 trang 69 Toán 7 Tập 1 Kết nối tri thức

Phân Tích và Hướng Dẫn Giải:

Để tính số đo các góc còn lại, ta sẽ áp dụng các định lý sau:

Tổng ba góc của một tam giác: Tổng ba góc trong một tam giác bằng $18 0^{\circ}$ . Công thức: $\widehat{A} + \widehat{B} + \widehat{C} = 180^\circ$.
Góc ngoài của tam giác: Góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.Ví dụ: $\widehat{AMB}$ là góc ngoài tại đỉnh M của tam giác $\Delta AMC$.

Chúng ta sẽ lần lượt tính số đo của từng góc theo một trình tự hợp lý.

Lời giải chi tiết:

Xét ΔAMC có: $\small \widehat{AMC}+\widehat{ACM}+\widehat{MAC}=180^0$

Nên: $\small \widehat{MAC}=180^0-(\widehat{AMC}+\widehat{ACM})$ $\small =180^0-(80^0+60^0)=40^0$

Mà $\small \widehat{AMB}$ là góc ngoài tại đỉnh M của ΔAMC nên

$\small \widehat{AMB}=\widehat{ACM}+\widehat{MAC}=60^0+40^0=100^0$

Xét ΔAMB có: $\small \widehat{AMB}+\widehat{MAB}+\widehat{ABM}=180^0$

Nên: $\small \widehat{ABM}=180^0-(\widehat{AMB}+\widehat{MAB})$ $\small =180^0-(100^0+20^0)=60^0$

hay $\small \widehat{ABC}=60^0$

Ta có: $\small \widehat{BAC}=\widehat{MAB}+\widehat{MAC}=20^0+40^0=60^0$

Vây $\small \widehat{AMB}=100^0;\: \: \widehat{ABC}=60^0;\: \: \widehat{BAC}=60^0$

Qua bài 4.10, các em đã rèn luyện được kỹ năng tính số đo góc bằng cách áp dụng một cách linh hoạt các định lý về góc kề bù, tổng ba góc trong tam giác. Việc nắm vững các định lý này là chìa khóa để giải quyết các bài toán hình học phức tạp hơn. Chúc các em học tốt và thành công!

• Xem thêm:

Bài 4.7 trang 69 Toán 7 Tập 1 Kết nối tri thức: Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?...

Bài 4.8 trang 69 Toán 7 Tập 1 Kết nối tri thức: Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông...

Bài 4.9 trang 69 Toán 7 Tập 1 Kết nối tri thức: Cho Hình 4.25, biết góc DAC = 60⁰, AB = AC, DB = DC. Hãy tính góc DAB...

Bài 4.11 trang 69 Toán 7 Tập 1 Kết nối tri thức: Cho ΔABC = ΔDEF. Biết rằng góc A = 60⁰ góc E = 80⁰. Tính số đo các góc B, C, D, F.