Giải bài 3.33 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Chào các em! Hôm nay chúng ta sẽ cùng giải một bài toán lý thuyết hình học quan trọng trong sách giáo khoa Toán 7 tập 1, bộ sách Kết nối tri thức. Bài 3.22 trang 54 sẽ giúp các em củng cố kiến thức về tiên đề Euclid về đường thẳng song song, một trong những nền tảng của hình học.
Đề bài:
Vẽ ba đường thẳng phân biệt a, b, c sao cho a // b, b // c và hai đường thẳng phân biệt m, n cùng vuông góc với a. Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc?
Phân tích và Phương pháp giải
Đề bài yêu cầu chúng ta xác định số lượng đường thẳng a và b có thể vẽ được.
-
Đường thẳng a: đi qua điểm A và song song với đoạn thẳng BC.
-
Đường thẳng b: đi qua điểm B và song song với đoạn thẳng AC.
Để giải quyết bài toán này, chúng ta cần nhớ lại một tiên đề cơ bản trong hình học, thường được gọi là Tiên đề Euclid về đường thẳng song song.
-
Nội dung tiên đề: Qua một điểm nằm ngoài một đường thẳng, chỉ có duy nhất một đường thẳng đi qua điểm đó và song song với đường thẳng đã cho.
Áp dụng tiên đề này, chúng ta có thể dễ dàng xác định được số lượng đường thẳng a và b cần tìm.
Lời giải chi tiết bài 3.33 trang 59 Toán 7:
Ta có hình minh họa như sau:
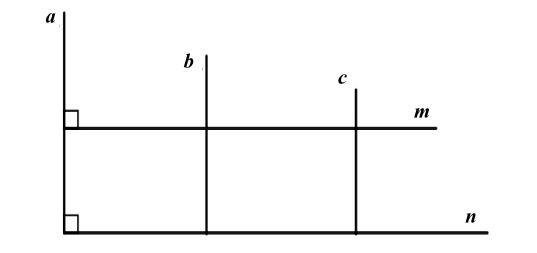
Vì a // b, b // c nên a // c.
Vì m ⊥ a; n ⊥ a nên m // n.
Các cặp đường thẳng song song là: (a, b); (b, c); (a, c); (m, n).
⇒ Trên hình có 4 cặp đường thẳng song song.
Vì a // b, m ⊥ a, nên m ⊥ b
Vì a // c, m ⊥ a nên m ⊥ c
Vì a // b, n ⊥ a nên n ⊥ b
Vì a // c, n ⊥ a nên n ⊥ c
Các cặp đường thẳng vuông góc là: (m, a); (m, b); (m, c) (n, a) (n, b) (n, c).
⇒ Trên hình có 6 cặp đường thẳng vuông góc.
Qua bài toán này, các em đã được ôn tập về một trong những tiên đề quan trọng nhất của hình học. Hãy luôn nhớ rằng, qua một điểm nằm ngoài một đường thẳng, chỉ có duy nhất một đường thẳng song song với đường thẳng đó. Kiến thức này sẽ là nền tảng vững chắc để các em học tốt hơn các bài hình học trong tương lai.
• Xem thêm:
Đánh giá & nhận xét
-
 Giải bài 4.11 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.11 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.10 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.10 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.9 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.9 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.8 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.8 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.7 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.7 trang 69 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.6 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.6 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.5 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.5 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.4 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.4 trang 67 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.3 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.3 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.2 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.2 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 4.1 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 4.1 trang 62 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.36 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.36 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.35 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.35 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.34 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.34 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.32 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.32 trang 59 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.31 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.31 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.30 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.30 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.29 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.29 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.28 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.28 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.27 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.27 trang 58 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.26 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.26 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.25 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.25 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.24 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.24 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.23 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.23 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.22 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.22 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.21 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.21 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.20 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.20 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.19 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức: Đường thẳng song song
Giải bài 3.19 trang 54 Toán 7 Tập 1 SGK Kết nối tri thức: Đường thẳng song song
-
 Giải bài 3.18 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.18 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.17 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.17 trang 53 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.16 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
Giải bài 3.16 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
-
 Giải bài 3.15 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.15 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.14 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.14 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.13 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.13 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.12 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.12 trang 50 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.11 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.11 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.10 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
Giải bài 3.10 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức: Hai đường thẳng song song
-
 Giải bài 3.9 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.9 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.8 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức
Giải bài 3.8 trang 49 Toán 7 Tập 1 SGK Kết nối tri thức


















































