Giải bài 3.26 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức

Bài 3.26 trang 57 Toán 7 Tập 1 Kết nối tri thức:

Cho góc xOy không phải góc bẹt. Khẳng định nào sau đây là đúng?

(1) Nếu Ot là tia phân giác của góc xOy thì 

(2) Nếu tia Ot thỏa mãn  thì Ot là tia phân giác của góc xOy.

Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng.

(Gợi ý: Xét tia đối của một tia phân giác).

Giải bài 3.26 trang 57 Toán 7 Tập 1 Kết nối tri thức:

Khẳng định (1) đúng dựa vào tính chất tia phân giác của góc.

Khẳng định (2) sai, ta có ví dụ minh hoạ như sau:

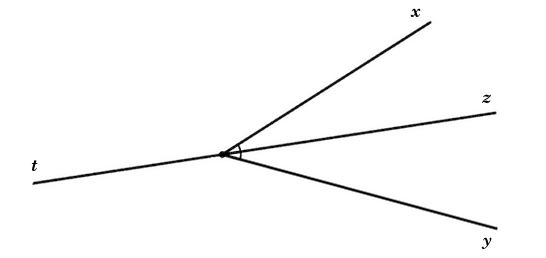
Trong hình vẽ trên, Oz là tia phân giác của góc xOy, Ot là tia đối của Oz.

Vì Oz là tia phân giác của góc xOy nên:

  (tính chất tia phân giác của góc).

Mà  và  (hai góc kề bù)

Ta thấy  mà Ot không phải tia phân giác của góc xOy nên khẳng định (2) sai.