Giải bài 3.25 trang 57 Toán 7 Tập 1 SGK Kết nối tri thức

Bài 3.25 trang 57 Toán 7 Tập 1 Kết nối tri thức:

Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?

Giải bài 3.25 trang 57 Toán 7 Tập 1 Kết nối tri thức:

Ta có hình minh hoạ sau:

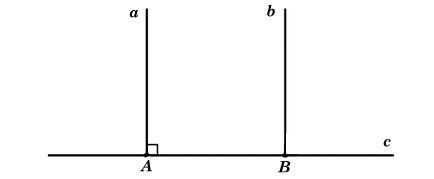
Trong hình vẽ trên, ta có hai đường thẳng a và b song song với nhau.

Đường thẳng c vuông góc với đường thẳng a.

Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.

Vì đường thẳng a vuông góc với đường thẳng c nên 

Vì đường thẳng a song song với đường thẳng b nên   (hai góc đồng vị)

Vậy đường thẳng b vuông góc với đường thẳng c.

Ở chứng minh trên, chúng ta sử dụng các kiến thức về số đo của góc vuông, các góc tạo bởi hai đường thẳng cắt nhau, tính chất hai đường thẳng song song.