Bài 1.6 trang 14 Toán 12 tập 1 Kết nối tri thức

Bài 1.6 trang 14 Toán 12:

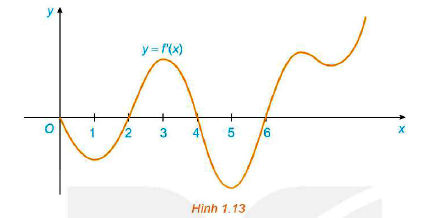
Đồ thị của đạo hàm bậc nhất y = f'(x) của hàm số f(x) được cho trong Hình 1.13:

a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.

b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.

Phân tích và Hướng dẫn giải

Để giải bài toán này, các em cần nhớ mối liên hệ cơ bản giữa dấu của đạo hàm f′(x) và sự biến thiên của hàm số $f(x)$:

• Hàm số $f(x)$ đồng biến trên một khoảng khi và chỉ khi đạo hàm f′(x)>0 trên khoảng đó.

• Hàm số $f(x)$ nghịch biến trên một khoảng khi và chỉ khi đạo hàm f′(x)<0 trên khoảng đó.

• Hàm số $f(x)$ đạt cực trị tại điểm x0​ nếu f′(x0​)=0 và f′(x) đổi dấu khi đi qua x0​.

  • $f(x)$ đạt cực đại nếu f′(x) đổi dấu từ dương sang âm.

  • $f(x)$ đạt cực tiểu nếu f′(x) đổi dấu từ âm sang dương.

Dựa vào đồ thị của y=f′(x), chúng ta sẽ xác định các khoảng mà f′(x) nằm trên (hoặc dưới) trục hoành để tìm dấu của nó.

Lời giải chi tiết:

a) Vì f'(x) > 0 khi x ∈ (2; 4) và x ∈ (6; +∞). 

Nên hàm số f(x) đồng biến trên (2; 4) và (6; +∞).

Vì f'(x) < 0 khi x ∈ (0; 2) và x ∈ (4; 6). 

Nên hàm số f(x) nghịch biến trên (0; 2) và (4; 6). 

b) Vì f'(x) < 0 với mọi x ∈ (0; 2) và f'(x) > 0 với mọi x ∈ (2; 4) thì x = 2 là một điểm cực tiểu của hàm số f(x).

Vì f'(x) > 0 với mọi x ∈ (2; 4) và f'(x) < 0 với mọi x ∈ (4; 6) thì điểm x = 4 là một điểm cực đại của hàm số f(x).

Vì f'(x) < 0 với mọi x ∈ (4; 6) và f'(x) > 0 với mọi x ∈ (6; +∞) thì x = 6 là một điểm cực tiểu của hàm số f(x).