Giải bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều
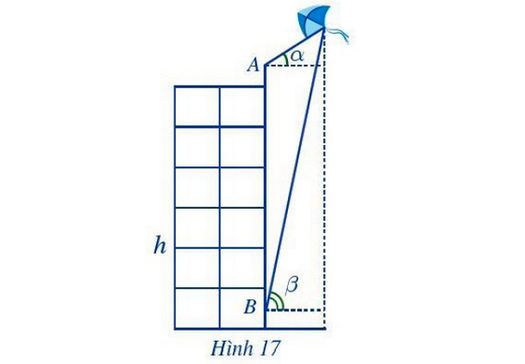
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều...
Bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều:
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là α = 35°;
khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là β = 75°;
khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng đơn vị)?
Giải bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều:
Ta đặt tên các điểm như trên hình sau:
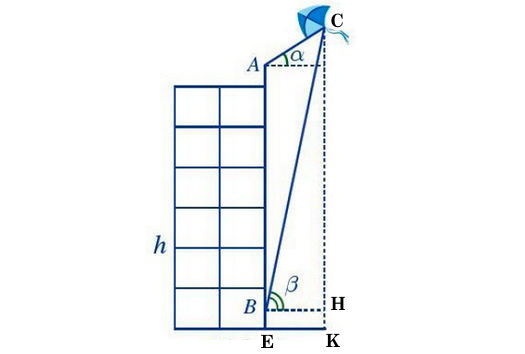
Ta có: AI là khoảng cách từ đỉnh của tòa nhà tới mắt bạn A nên AI = 1,5 m.
BE là khoảng cách từ mặt đất tới mắt của bạn B nên BE = 1,5 m.
Lại có: h = IB + BE ⇒ IB = h – BE = 20 – 1,5 = 18,5 (m).
Và AB = AI + IB = 1,5 + 18,5 = 20 (m)
Ta có:
Theo định lí tổng ba góc trong ΔABC có:
Áp dụng định lí sin trong ΔABC ta có:
Xét ΔCBH vuông tại H nên:
⇒ CH = BC . sin β = 25,5 . sin 75° ≈ 24,6.
Lại có: HK = BE = 1,5 m.
Do đó CK = CH + HK = 24,6 + 1,5 = 26,1 (m).
Vậy chiếc diều bay cao 26,1 m so với mặt đất.
Với nội dung bài 1 tráng 71 Toán 10 tập 1 Cánh diều cùng cách giải bài 1 trang 71 Toán 10 Tập 1 Cánh Diều chi tiết, dễ hiểu. Hay Học Hỏi hy vọng giúp các em nắm vững cách giải Toán 6 tập 1 SGK cánh diều. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.
• Xem giải bài tập Toán 10 tập 1 SGK Cánh Diều cùng chuyên mục
> Bài 2 trang 71 Toán 10 Tập 1 SGK Cánh Diều: Cho tam giác ABC có ,
và BC = 50. Tính độ dài cạnh AB.
> Bài 5 trang 71 Toán 10 Tập 1 SGK Cánh Diều: Cho tam giác ABC. Chứng minh:...
Đánh giá & nhận xét
-
 Giải bài 6 trang 43 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 43 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 43 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 43 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 43 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 43 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 43 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 43 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 43 Toán 10 Tập 1 SGK Cánh Diều: Hàm số bậc hai
Giải bài 2 trang 43 Toán 10 Tập 1 SGK Cánh Diều: Hàm số bậc hai
-
 Giải bài 1 trang 43 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 43 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 9 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 9 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 58 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 58 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 11 Toán 10 tập 1 SGK Cánh Diều
Giải bài 7 trang 11 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 11 Toán 10 tập 1 SGK Cánh Diều
Giải bài 6 trang 11 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 11 Toán 10 tập 1 SGK Cánh Diều
Giải bài 5 trang 11 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 11 Toán 10 tập 1 SGK Cánh Diều
Giải bài 4 trang 11 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 11 Toán 10 tập 1 SGK Cánh Diều
Giải bài 3 trang 11 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 11 Toán 10 tập 1 SGK Cánh Diều
Giải bài 2 trang 11 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 11 Toán 10 tập 1 SGK Cánh Diều
Giải bài 1 trang 11 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 38 Toán 10 tập 1 SGK Cánh Diều
Giải bài 5 trang 38 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 24 Toán 10 tập 1 SGK Cánh Diều
Giải bài 5 trang 24 Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 54 Toán 10 Tập 1 SGK Cánh Diều: Giải bất phương trình
Giải bài 3 trang 54 Toán 10 Tập 1 SGK Cánh Diều: Giải bất phương trình
-
 Giải bài 3 trang 30 Toán 10 tập 1 SGK Cánh Diều: Bất phương trình bậc nhất 2 ẩn
Giải bài 3 trang 30 Toán 10 tập 1 SGK Cánh Diều: Bất phương trình bậc nhất 2 ẩn


















































