Giải bài 8 trang 20 Toán 11 tập 1 SGK Chân trời sáng tạo

Đề Bài 8 trang 20 Toán 11 tập 1:

Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13).

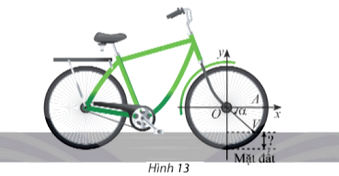
Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58 cm? Giả sử độ dày của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:

1. Tính tổng góc quay: Dùng công thức $\alpha =\omega \cdot t$ để tính tổng góc quay của van sau một phút, với $\omega$ là tốc độ góc và $t$ là thời gian.

2. Xác định vị trí:

   • Thiết lập một hệ tọa độ với gốc tại tâm bánh xe O.

   • Ban đầu, van ở vị trí A, là điểm cao nhất trên bánh xe. Sau khi quay, ta cần tìm tọa độ của van V.

3. Tính khoảng cách đến mặt đất: Khoảng cách từ van đến mặt đất bằng tổng bán kính của bánh xe (khoảng cách từ tâm O đến mặt đất) và chiều cao của van V so với tâm O.

Lời giải chi tiết:

Bước 1: Tính góc quay của van V

• Thời gian di chuyển là một phút, tức là $t=60$ giây.

• Tốc độ góc là $\omega =11$ rad/s.

• Tổng góc quay $\alpha$ là:

  $$\alpha =\omega \cdot t=11\cdot 60=660\text{ (rad)}$$

Bước 2: Xác định vị trí của van V

• Ta đặt hệ trục tọa độ với gốc tại tâm O của bánh xe, trục hoành nằm ngang và trục tung thẳng đứng.

• Vị trí ban đầu của van là điểm A trên trục hoành dương, tương ứng với góc $0$ rad.

• Van quay theo chiều kim đồng hồ, nên góc quay là âm. Vị trí cuối cùng của van V có góc là θ_cuối=0−660=−660 (rad).

• Chiều cao của van V so với tâm O chính là tọa độ yV​. Ta có công thức tọa độ của điểm trên đường tròn bán kính R là $(R\cos \theta ,R\sin \theta )$. Vậy, y_V​=Rsin(−660).

• Sử dụng tính chất hàm sin là hàm lẻ: $\sin (-x)=-\sin (x)$, ta có y_V​=−58sin(660).

Bước 3: Tính khoảng cách từ van đến mặt đất

• Khoảng cách từ van đến mặt đất là h=R+y_V​=58−58sin(660).

• Ta cần tính $\sin (660)$.

  $$660\approx 105,04\cdot 2\pi \text{ rad}$$

  

• Khoảng cách từ van đến mặt đất là:

  $$h\approx 58-58\cdot (0,266)=58-15,428\approx 42,572\text{ (cm)}$$

• Làm tròn đến hàng phần mười, ta có $h\approx 42,6$ cm.