Giải bài 9 trang 24 Toán 11 tập 1 SGK Chân trời sáng tạo

Đề bài:

Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là 2π/3 và số đo góc (OA, OM) là α.

a) Tính sinα và cosα.

b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:

• Xác định tọa độ: Mối quan hệ giữa tọa độ điểm trên mặt phẳng và giá trị lượng giác của góc là: $x=R\cos \alpha$ và $y=R\sin \alpha$. Trong bài toán này, bán kính $R$ chính là chiều dài cánh quạt.

• Sử dụng thông tin: Chiều cao của một điểm so với mặt đất bằng chiều cao của tâm quay cộng với tung độ của điểm đó trên hệ trục tọa độ.

• Áp dụng công thức: Sử dụng các công thức lượng giác để tìm giá trị cần thiết. Cần lưu ý các góc giữa các cánh quạt là $2\pi /3$.

Lời giải chi tiết:

a) Tính sinα và cosα

Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy.

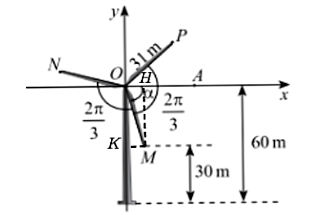
Ta có: MH = 60 – 30 = 30 m.

Khi đó tung độ điểm M là: y_M = -30.

Mà ta lại có: MH = OM.sinα = 31.sinα

Từ công thức: sin²α + cos²α = 1 nên có:

b) Vì các cánh quạt tạo thành 3 góc bằng nhau nên

Vì vậy chiều cao của điểm P so với mặt đất khoảng:

 31.sin(OA,OP) + 60 = 31.0,7+60 = 81,76 m.

và

Lại có: 

Vì vậy chiều cao của điểm N so với mặt đất khoảng:

31.sin(OA,ON) + 60 = 31.0,27 + 60 = 68,29 m.