Giải bài 8 trang 24 Toán 11 tập 1 SGK Chân trời sáng tạo: Ứng dụng lượng giác

Đề bài:

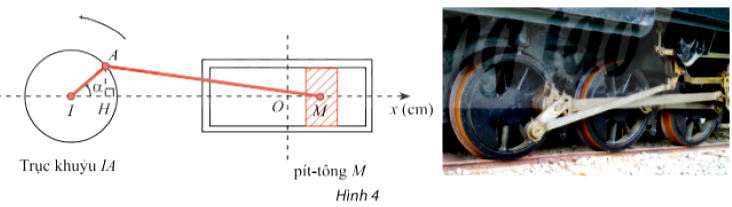
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng.

Cho α là góc quay của trục khuỷu, O là vị trí của pít – tông khi α = π/2 và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

a) Biết IA = 8cm, viết công thức tính tọa độ x_M của điểm M trên trục Ox theo α.

b) Ban đầu α = 0. Sau 1 phút chuyển động, x_M = – 3cm. Xác định x_M sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười.

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, chúng ta cần phân tích chuyển động và các yếu tố hình học liên quan.

• Phần a): Mục tiêu là tìm công thức tính tọa độ của điểm M (x_M​) theo góc quay $\alpha$ của trục khuỷu.

  • Ta có thể sử dụng hình chiếu A trên trục Ox để tạo thành một tam giác vuông.

  • Áp dụng các công thức lượng giác trong tam giác vuông đó để tìm mối liên hệ giữa tọa độ x_M​ và góc $\alpha$.

• Phần b): Dựa trên công thức ở phần a), chúng ta sẽ tính toán vị trí của pít-tông sau 2 phút chuyển động.

  • Sử dụng dữ liệu sau 1 phút để tìm giá trị của $\cos \alpha$.

  • Vì tốc độ quay không đổi, góc quay sau 2 phút sẽ là $2\alpha$.

  • Áp dụng công thức lượng giác thích hợp (công thức nhân đôi) để tính giá trị $\cos (2\alpha )$ và từ đó tìm ra x_M​.

Lời giải chi tiết bài 8 trang 24 Toán 11:

a) Tại α = π/2 thì H trùng I, M trùng O nên

 MH = OI ⇒ OM = IH.

Xét tam giác AHI vuông tại H có:

 IH = cosα.IA = 8cosα.

Tức là: x_M = OM = IH = 8cosα

b) Sau khi chuyển động 1 phút, trục khuỷu quay được một góc là α

Khi đó: x_M = -3cm, theo công thức trên ta:

Sau khi chuyển động 2 phút, trục khuỷu quay được một góc là 2α, nên:

Vậy, khi đó: