Giải bài 4 trang 29 Toán 10 tập 1 SGK Cánh Diều
Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất...
Bài 4 trang 29 Toán 10 tập 1 SGK Cánh Diều: Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc.
Phân xưởng làm việc không quá 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng.
Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.
Giải bài 4 trang 29 Toán 10 tập 1 SGK Cánh Diều:
- Gọi x, y lần lượt là số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được cao nhất. (với x, y ∈ N)
- Trong một ngày thị trường tiêu thụ tối đa 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai nên ta có:
0 ≤ x ≤ 200; 0 ≤ y ≤ 240.
- Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn và một chiếc mũ kiểu thứ hai là 15 nghìn nên tổng số tiền lãi khi bán mũ là:
T = 24x + 15y.
- Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong một giờ phân xưởng làm được 60 chiếc nên thời gian để làm một chiếc mũ kiểu thứ hai là: 1/60 (giờ).
- Thời gian làm ra một chiếc kiểu mũ thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai nên thời gian để làm một chiếc mũ kiểu thứ nhất là:
(giờ).
- Thời gian để làm x chiếc mũ kiểu thứ nhất là: (giờ)
- Thời gian để làm y chiếc mũ kiểu thứ hai là: (giờ).
Tổng thời gian để làm hai loại mũ trong một ngày là:
(giờ)
Vì một ngày phân xưởng làm việc không quá 8 tiếng nên:
Khi đó bài toán đã cho đưa về dạng tìm x, y là nghiệm của hệ bất phương trình:
sao cho T = 24x + 15y có giá trị lớn nhất.
→ Như vậy, trước tiên ta xác định miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là miền ngũ giác ABCDO với A(0; 240), B(120; 240), C(200; 80), D(200; 0), O(0; 0) như hình sau:
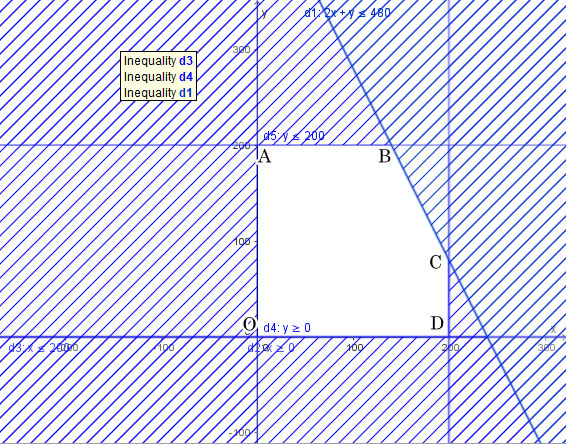
• Tại đỉnh A: T = 24 . 0 + 15 . 240 = 3600
• Tại đỉnh B: T = 24 . 120 + 15 . 240 = 6480
• Tại đỉnh C: T = 24 . 200 + 15 . 80 = 6000
• Tại đỉnh D: T = 24 . 200 + 15 . 0 = 4800
• Tại đỉnh O: T = 0
Vây ta có: 0 < 3600 < 4800 < 6000 < 6480
So sánh giá trị của biểu thức T tại các đỉnh, ta thấy T đạt giá trị lớn nhất bằng 6480 khi x 120 và y = 240 ứng với tọa độ đỉnh B.
⇒ Vậy để tiền lãi thu được là cao nhất, trong một ngày xưởng cần sản xuất 120 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Khi đó tiền lãi là 6480 nghìn đồng hay 6 480 000 đồng.
Hy vọng với lời giải bài 4 trang 29 SGK Toán 10 tập 1 Cánh Diều ở trên đã giúp các em hiểu và nắm vững phần kiến thức này. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Hay Học Hỏi ghi nhận và hỗ trợ, chúc các em học tốt.
• Xem các bài tập Toán 10 tập 1 SGK Cánh Diều cùng chuyên mục
> Bài 2 trang 29 Toán 10 tập 1 SGK Cánh Diều: Biểu diễn miền nghiệm của hệ bất phương trình:...
Đánh giá & nhận xét
-
 Giải bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải Bài tập Toán 10 tập 1 SGK Cánh Diều
Giải Bài tập Toán 10 tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 9 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 9 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 58 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 58 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 48 Toán 10 Tập 1 SGK Cánh Diều


















































