Giải Toán 8 trang 76 tập 2 Chân trời sáng tạo

Bài 2 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Quan sát hình 9

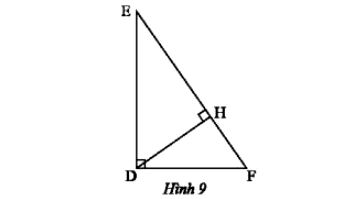
a) Chứng minh rằng ΔDEF ᔕ ΔHDF.

b) Chứng minh DF² = FH.FE.

c) Biết EF = 15 cm, FH = 5,4 cm. Tính độ dài đoạn thẳng DF.

> Giải bài 2 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 3 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

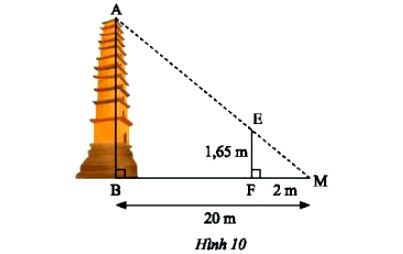
Trong Hình 10, biết MB = 20m, MF = 2m, EF = 1,65 m. Tính chiều cao AB của ngọn tháp.

> Giải bài 3 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 4 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Trong Hình 11, cho biết  , BE = 25 cm, AB = 20 cm, DC = 15 cm. Tính độ dài đoạn thẳng CE.

> Giải bài 4 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 5 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Quan sát Hình 12. Chứng minh rằng:

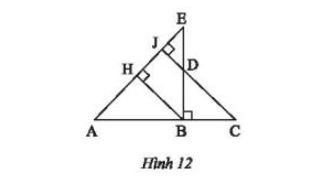
a) ΔABH ᔕ ΔDCB.

b) BC/BE = BD/BA

> Giải bài 5 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 6 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3 m và đặt cách xa tòa nhà 27 m. Sau khi người ấy lùi ra xa cách cọc 1,2 m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng nằm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5 m.

> Giải bài 6 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 7 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HM vuông góc với AB tại M.

a) Chứng minh rằng ΔAMH ᔕ ΔAHB.

b) Kẻ HN vuông góc với AC tại N. Chứng minh rằng AM.AB = AN.AC.

c) Chứng minh rằng ΔANM ᔕ ΔABC.

d) Cho biết AB = 9 cm, AC = 12 cm. Tính diện tích tam giác AMH.

> Giải bài 7 trang 76 Toán 8 Tập 2 Chân trời sáng tạo