Giải bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo

Bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo: Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I≠C), EG cắt AD tại H (H≠D)

a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD); (EFG) và (ACD)

b) Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm

Giải bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo:

a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD); (EFG) và (ACD)

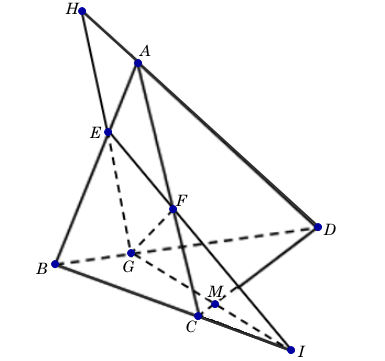
Ta có I và G là hai điểm chung của mặt phẳng (EFG) và (BCD)

nên GI là giao tuyến của (EFG) và (BCD)

Gọi M là giao điểm của GI và CD, khi đó

CD ⊂ (ACD) nên M ∈ (ACD)

Ta có M và F là điểm chung của mặt phẳng (EFG) và (ACD)

nên MF là giao tuyến của (EFG) và (ACD)

b) Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm

Ta có H ∈ AD mà AD⊂(ACD) nên H ∈ (ACD)

H ∈ EG mà EG ⊂ (EFG) nên H ∈ (EFG)

⇒ H là giao điểm của (EFG) và (ACD)

nên H nằm trên giao tuyến của (EFG) và (ACD): H ∈ FM.

Hay HF đi qua M.

Do đó, CD, IG, HF cùng đi qua điểm M.