Giải bài 2 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo

Bài 2 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC.

a) Tìm giao điểm I của đường thẳng AM và mặt phẳng (SBD). Chứng minh IA = 2IM.

b) Tìm giao điểm E của đường thẳng SD và mặt phẳng (ABM).

c) Gọi N là một điểm tuỳ ý trên cạnh AB. Tìm giao điểm của đường thẳng MN và mặt phẳng (SBD)

Giải bài 2 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo:

Ta có hình vẽ minh hoạ như sau: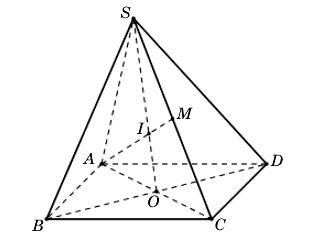

a) Gọi I là giao điểm của SO và AM.

+) Ta có: I ∈ AM

Do I ∈ SO mà SO ⊂ (SBD) nên I ∈ (SBD)

Vậy I giao điểm của AM và (SBD)

+) Xét ΔSAC, ta có:

M là trung điểm của SC,

O là trung điểm của AC

nên SO cắt AM tại I là trọng tâm của ΔSAC

Suy ra:  hay

b) Trên mặt phẳng (SCD) kẻ một đường thẳng song song với AB cắt SD tại E.

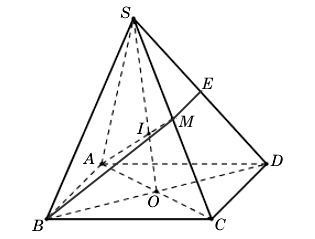
Vì ME//AB nên A,B,M,E cùng thuộc một mặt phẳng,

hay E ∈ (ABM)

Vậy E là giao của (ABM) và SD

c) N là một điểm tuỳ ý trên cạnh AB.

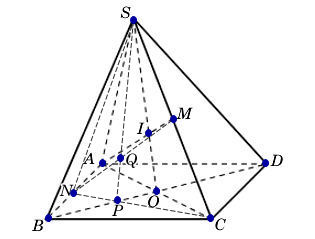
Trong mặt phẳng (ABCD), gọi NC cắt BD tại P. 

Ta có S và P là hai điểm chung của hai mặt phẳng (SNC) và (SBD)

Nên SP là giao tuyến của (SNC) và (SBD).

Trong mặt phẳng (SNC), gọi MN cắt SP tại Q. 

Do SP ⊂ (SBD) nên Q ∈ (SBQ)

Vậy giao điểm của MN và (SBD) là Q