Giải bài 4 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo

Bài 4 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo: Cho tứ diện ABCD và điểm M thuộc cạnh AB. Gọi (α) là mặt phẳng qua M, song song với hai đường thẳng BC và AD. Gọi N, P, Q lần lượt là giao điểm của mặt phẳng (α) với các cạnh AC, CD và BD.

a) Chứng minh MNPQ là hình bình hành

b) Trong trường hợp nào thì MNPQ là hình thoi?

Giải bài 4 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

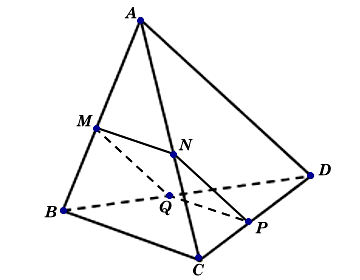
a) Ta có: (α)//BC; BC ⊂ (ABC) và (α) cắt (ABC) tại MN nên MN//BC

(α)//BC; BC ⊂ (BCD) và (α) cắt (BCD) tại PQ nên PQ//BC

Vậy, nên: MN//PQ

Lại có: (α)//AD; AD ⊂ (ABD) và (α) cắt (ABD) tại MQ nên MQ//AD

(α)//AD; AD ⊂ (ACD) và (α) cắt (ACD) tại NP nên NP//BC

Vậy nên: MQ//NP

Từ đó, suy ra: MNPQ là hình bình hành

b) hình bình hành MNPQ là hình thoi khi MN = NP

Vì ΔAMN ~ ΔABC nên: 

Vì ΔCNP ~ ΔCAD nên:  

Mà MN = NP nên có: 

Mà  nên