Bài 4.19 Toán 9 tập 1 SGK Kết nối tri thức

Đề bài 4.19 - SGK Toán 9 Tập 1 Kết nối tri thức:

Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt bên AB của đạp là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).

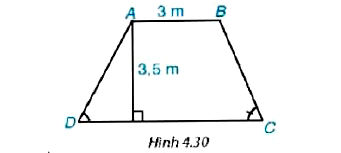
Hướng dẫn giải chi tiết bài 4.19 SGK Toán 9 Tập 1:

Ta có hình:

Kẻ AE ⊥ CD, BF ⊥ CD. Khi đó AE // BF.

Vì ABCD là hình thang nên AB // CD, do đó suy ra AB // EF.

Xét tứ giác ABFE có: AE // BF và AB // EF nên là hình bình hành.

Lại có   nên hình bình hành ABFE là hình chữ nhật.

Suy ra EF = AB = 3 m.

Xét ∆ADE vuông tại E, ta có: 

Vì ABFE là hình chữ nhật nên BF = AE = 3,5 m.

Xét ∆BCF vuông tại F, ta có:

Ta có: DC = DE + EF + FC = 2,8 + 3 +7/3 = 122/15 = 8,1(3) (m) ≈ 81(dm)

Xét ∆ADE vuông tại E, theo định lí Pythagore, ta có:

AD² = AE² + DE² = 3,5² + 2,8² = 20,09.

Suy ra 

Xét ∆BCF vuông tại F, theo định lí Pythagore, ta có:

Suy ra: 

Vậy AD ≈ 45 dm, BC ≈ 42 dm.