Giải bài 2 trang 53 Toán 7 Tập 1 SGK Chân trời sáng tạo: Hình hộp chữ nhật

Đề bài:

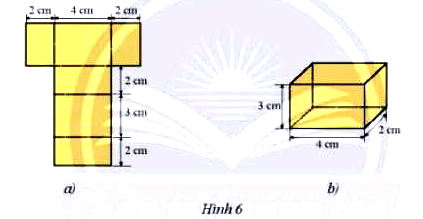
Hãy vẽ và gấp tấm bìa như Hình 6a thành một hình hộp chữ nhật như Hình 6b. Tính tổng diện tích các mặt và thể tích của hình hộp.

Phân tích và Hướng dẫn giải

Để giải bài toán này, chúng ta cần xác định các kích thước của hình hộp chữ nhật từ tấm bìa đã cho. Quan sát Hình 6a, ta có thể thấy các kích thước cơ bản của hình hộp:

• Chiều dài (a): 4 cm

• Chiều rộng (b): 2 cm

• Chiều cao (h): 3 cm

Sau khi đã xác định được ba kích thước này, ta áp dụng các công thức sau để tính toán:

• Tổng diện tích các mặt (Diện tích toàn phần): Tổng diện tích các mặt của hình hộp chữ nhật bằng tổng diện tích của 6 mặt (3 cặp mặt đối diện có diện tích bằng nhau).

  Công thức là:

  S_tp​=2(ab+ah+bh)

  Hoặc cách khác là tổng diện tích xung quanh và diện tích hai mặt đáy:

  S_tp​ =S_xq​+2S_đaˊy​ =2h(a+b)+2ab

• Thể tích (V): Thể tích của hình hộp chữ nhật bằng tích của chiều dài, chiều rộng và chiều cao. Công thức là:

  $V=a\cdot b\cdot h$

Lời giải chi tiết:

• Diện tích toàn phần của hình hộp chữ nhật bằng diện tích xung quanh cộng với diện tích 2 mặt đáy.

S_tp = 2h(a + b) + 2ab.

(với a, b, h lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật).

Cắt tấm bìa theo các kích thước như Hình 6a. Sau đó gấp theo đường kẻ đậm ta được Hình 6b.

• Tổng diện tích các mặt của hình hộp chữ nhật là:

 2.3.(4 + 2) + 2.4.2 = 52 (cm²).

• Thể tích của hình hộp chữ nhật là:

 4.2.3 = 24 (cm³).

→ Tổng diện tích các mặt và thể tích của hình hộp chữ nhật lần lượt là 52 cm² và 24 cm³.