Bài 2 trang 64 Toán 11 tập 2 Chân trời sáng tạo

Bài 2 trang 64 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Chứng minh rằng:

a) AC ⊥ (SHK) ;

b) CK ⊥ (SDH) .

Giải bài 2 trang 64 Toán 11 tập 2 Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

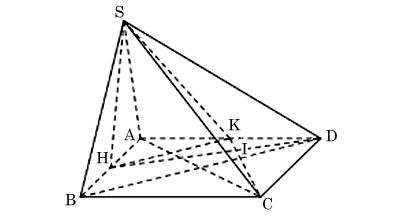
a) Xét tam giác ADB:

H là trung điểm AB

K là trung điểm AD

⇒ HK là đường trung bình của ΔADB.

Suy ra: HK // BD và AC ⊥ BD

Suy ra: AC ⊥ HK

Ta có:

AC ⊥  HK

Mà SH ⊥ (ABCD) nên SH ⊥  AC

Suy ra: AC ⊥ (SHK)

b) Gọi là giao của CK và DH

Xét ΔAHD và ΔDKC:

AH = DK

AD = CD

⇒ ΔAHD = ΔDKC (c.g.c)

Suy ra: 

Ta có:

Suy ra: 

⇒ DH ⊥ CK

Mà SH ⊥ (ABCD) ⇒ SH ⊥ CK

Vậy CK ⊥ (SDH).