Bài 1.5 trang 10 Toán 9 tập 1 Kết nối tri thức SGK

Đề Bài 1.5 trang 10 Toán 9:

Cho các cặp số (–2; 1), (0; 2), (1; 0), (1,5; 3), (4; –3) và hai phương trình:

5x + 4y = 8,    (1)

3x + 5y = –3,  (2)

Trong các cặp số đã cho:

a) Những cặp số nào là nghiệm của phương trình (1)?

b) Những cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?

c) Vẽ hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3 trên cùng một mặt phẳng toạ độ để minh hoạ kết luận ở câu b.

Phân tích và Hướng dẫn giải

Bài toán này gồm ba yêu cầu chính:

1. Tìm nghiệm của phương trình (1): Các em sẽ lần lượt thay từng cặp số vào phương trình (1). Nếu đẳng thức đúng, cặp số đó là nghiệm.

2. Tìm nghiệm của hệ phương trình: Dựa vào kết quả ở câu a, ta chỉ cần kiểm tra những cặp số là nghiệm của phương trình (1) xem chúng có là nghiệm của phương trình (2) hay không. Nếu thỏa mãn cả hai, đó là nghiệm của hệ.

3. Biểu diễn hình học: Vẽ hai đường thẳng tương ứng với hai phương trình trên cùng một mặt phẳng tọa độ. Giao điểm của hai đường thẳng chính là nghiệm của hệ phương trình.

Lời giải chi tiết:

a) Những cặp số nào là nghiệm của phương trình (1)

Ta lần lượt thay giá trị các cặp số (–2; 1), (0; 2), (1; 0), (1,5; 3), (4; –3) vào phương trình 5x + 4y = 8

Với cặp số (–2; 1), ta có: 5.(–2) + 4.1 = –10 + 4 = –6 ≠ 8 không phải là nghiệm của (1)

Với cặp số (0; 2), ta có: 5.0 + 4.2 = 0 + 8 = 8 là nghiệm của (1)

Với cặp số (1; 0), ta có: 5.1 + 4.0 = 5 + 0 = 5 ≠ 8 không phải là nghiệm của (1)

Với cặp số (1,5; 3), ta có: 5.1,5 + 4.3 = 7,5 + 12 = 19,5 ≠ 8 không phải là nghiệm của (1)

Với cặp số (4; –3), ta có: 5.4 + 4.(–3) = 20 – 12 = 8 là nghiệm của (1)

Vậy (0; 2) và (4; –3) là các cặp nghiệm của (1): 5x + 4y = 8.

b) Những cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?

Theo câu a) giờ để cặp nghiệm của hệ phương trình (1) và (2) ta chỉ cần kiểm tra các cặp nghiệm của (1) có thoả phương trình (2) hay không.

+ Với cặp (0; 2) thay vào phương trình: 3x + 5y = –3

Ta được: 3.0 + 5.2 = 10 ≠ –3 Không phải là cặp nghiệm của (2)

+ Với cặp (4; –3) thay vào phương trình: 3x + 5y = –3

Ta được: 3.4 + 5.(–3) = –3 là cặp nghiệm của (2)

→ Vậy cặp (4; –3) là nghiệm của hệ hai phương trình (1) và (2).

c) Vẽ hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3 trên cùng một mặt phẳng toạ độ

Viết 5x + 4y = 8 về dạng: y = –5x/4 + 2

Lấy hai điểm chẳng hạn là A(0; 2) và B(8/5; 0)

Viết 3x + 5y = –3 về dạng: y = –3x/5 – 3/5

Lấy hai điểm chẳng hạn là C(0; –3/5) và B(–1; 0)

Ta vẽ được hai đường thẳng như sau:

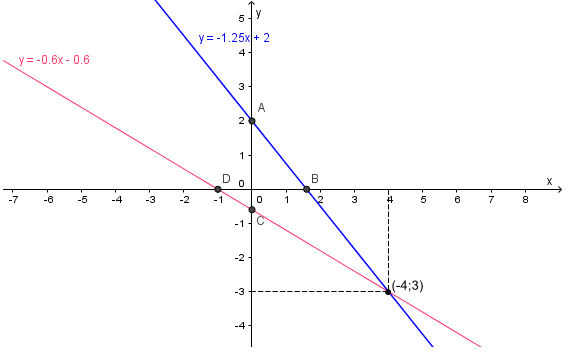
Như vậy ta thấy hai đường thẳng cắt nhau tại điểm có toạ độ (–4; 3) chính là nghiệm của hệ phương trình (1) và (2) ở câu b.